You were going to give us an example of a good problem.
Here is a good problem for students tackling percentages, and probability. The problem takes an hour or two…
This is an example of some cipher-text created from a Polybius Square. The Germans used a variant of this cipher in World War I.
AG DG DD DD DA DD FF GX DG XD GD DD GF DX AG DG XX AF XD GF DA AA AF AD FF AG DG DD AG AF DD DA XG DG DX DA AA AF AD DA AG AD AA AD AX AF FG AD GA DX AG DX AD DA GF DD XD AF DD XD XX GD XD DA XG DX DA DF AG AD AD XG XG AX FG GX AG DG DX GA AG AF DD DA XG DG GA AG XD AF AG DX DA DF DX FF FF DD XX DX XD AG DD FD GX
Decipher it.
Surely you’re joking. That looks impossibly difficult to solve – and I don’t understand the connection to probability or percentages.
The students might start by making small discoveries. If they get stalled, you generously help them through the engagement-phase.
Generous Help #1: There are only 5 letters used in the cipher-text.
Generous Help #2: There are 5×5 = 25 possible two-letter combos of these letters.
Generous Help #3: This is pretty close to 26, the number of letters in our alphabet.
Generous Help #4: Maybe each two-letter combo represents a single letter when deciphered
Generous Help #5: Since we don’t have quite enough two-letter combos in our cipher-text, two letters (i/j) of our alphabet will be represented by the same two letter combo in the cipher-text.
Generous Help #6: We just have to figure out how to place the letters on the right into the grid on the left.
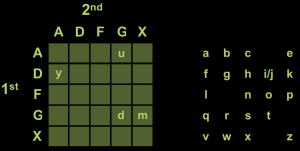
Generous Help #7: For example “muddy” would have the cipher-text “GX AG GG GG DA” if m = GX, u = AG, d = GG and y = DA.
This is just an example – the cipher-text that you are trying to break does not necessarily have m = GX, u = AG, d = GG, and y = DA.
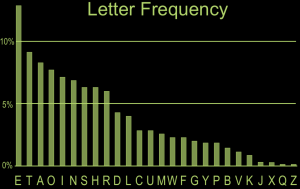
The probability comes into play when you start to observe that the two-letter combos in the cipher-text have different frequencies. AG and DD are the most common and other combinations like FA and FX don’t appear at all. These are clues that help the deciphering. When the students start to talk about letter frequency in English you present them with the following graph:
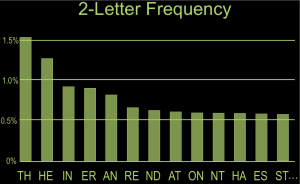
Now that you’ve got the students engaged, they split off into small groups to tackle the problem. Your generosity plummets. Be as helpless as you can! The one exception is if you can gently help a group of students to realize that additional statistics would help. Handing out a new frequency table to a few groups is a good way to maintain engagement. The one below describes the most common two-letter combinations in English.
The actual cipher used by the Germans was more complicated, but was eventually cracked by French Army Lieutenant Georges Painvin. I always mention war if I have the opportunity, because that engages the half of the class with excess testosterone 😉
Much thanks to Alessandro Nastri for the cover photo of Enigma (CC BY-SA 4.0)

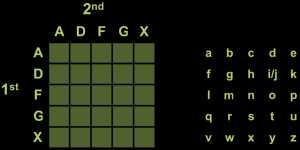

Pretty! This has been an extremely wonderful post. Thanks for providing these details.|