Cardboard Snowflakes (calculating average)

Cardboard Snowflakes are created by putting a non-negative integer in each circle. There can be no duplicates. Circles are the average of all smaller circles touching them. Here we have failed. Can you find out why?

Part of the snowflake looks good. 7 is the average of 4, 6 and 11. 2 is the average of 0, 1 and 5. 14 is the average of 3, 21, and 18. The failure is that 8 is not the average of 14, 7 and 2.

Find a solution with the smallest possible integer in the centre. That’s the objective. On the next slide (which you should definitely NOT show to your class) you will see the best solution that I found with a half hour of searching. It is probably the best possible…

Six is probably the smallest integer that can be in the centre. I have not put a half hour effort into solving the other cardboard snowflakes that you will see on the puzzle sheet on the next slide.

This is the first puzzle sheet. You can download all puzzle sheets at the end of this slide show.

This is the second puzzle sheet. On the following slide we will climb one of the cardboard mountains. Again, each circle on a mountain must be filled with a unique, non-negative integer. Each circle is the average of the lower circles that it touches. The objective is to find the smallest possible number at the peak.

Here we have successfully climbed a cardboard mountain. 5 is the average of 0 and 10… 9 is the average of 5 and 13… 12 is the average of 9 and 15.

But is 12 as small as possible? Certainly not! Your students should try to find a solution with a smaller number at the peak. Do not let your students see the following two slides without them trying to solve this.

The best that I could do was to get 6 on top. This took me half an hour to find. On the next slide you’ll see my solution.

Again, I’m pretty sure this is optimal, but I’ve made so many mistakes stating false conclusions, that you should always treat my assertions with suspicion 😉

A much more beautiful conjecture by Ryan Hauge is that the optimal for any height of mountain is achieved by placing the triangle numbers up the left side. See the next page for his solution.

Ryan Hauge suggested that the optimal solution for a mountain is always a triangular number.

The last sheet is probably the easiest because all but the bottom right hill all probably optimally solvable by a simple pattern.

The following download includes the three puzzle sheets – ready for printing as well as two projectable images to practice solving as a class. Download here.

Cardboard Snowflakes

(MathPickle, 2015)

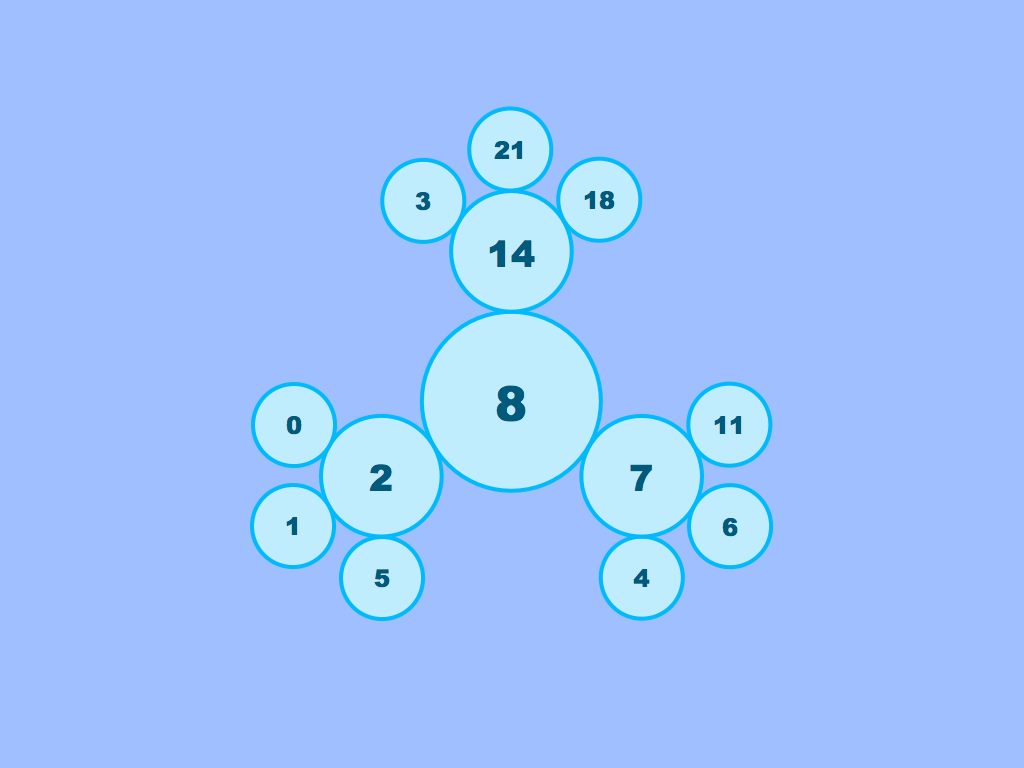
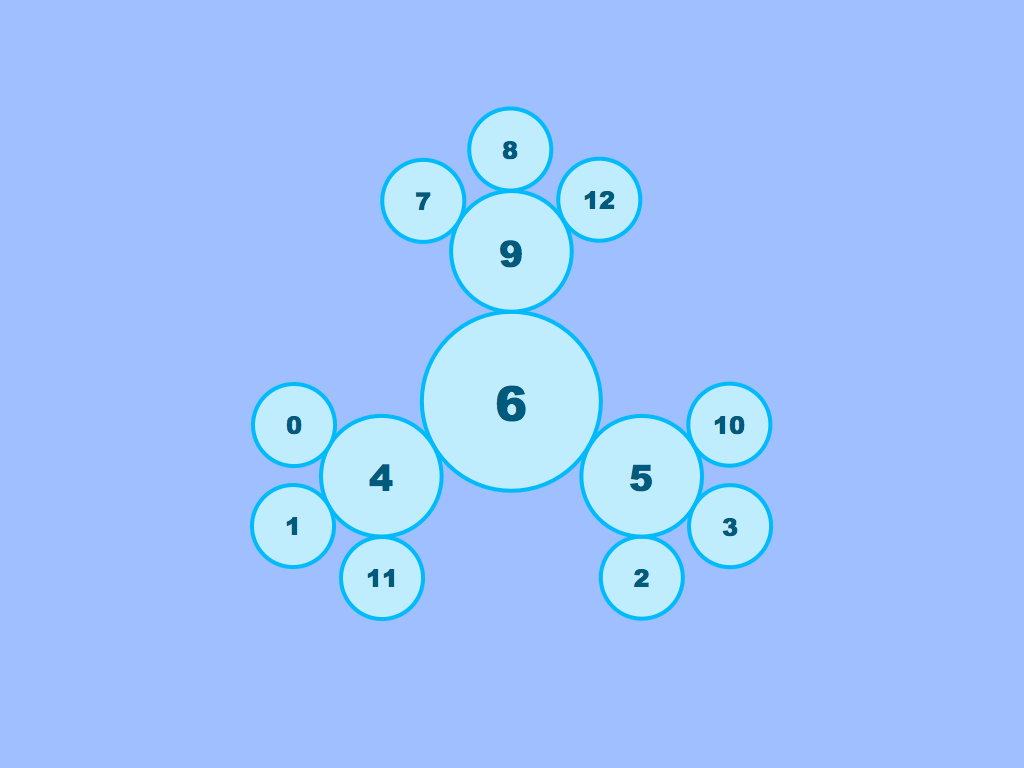
Give your students practice finding the average of some integers. As with nearly all MathPickle puzzles – most students should work in pairs with a single sheet in front of them. Keep the other two puzzle sheets hidden. These will re-engage students 15 minutes into the lesson. Keep the mystery alive 😉

There are three puzzle sheets included:

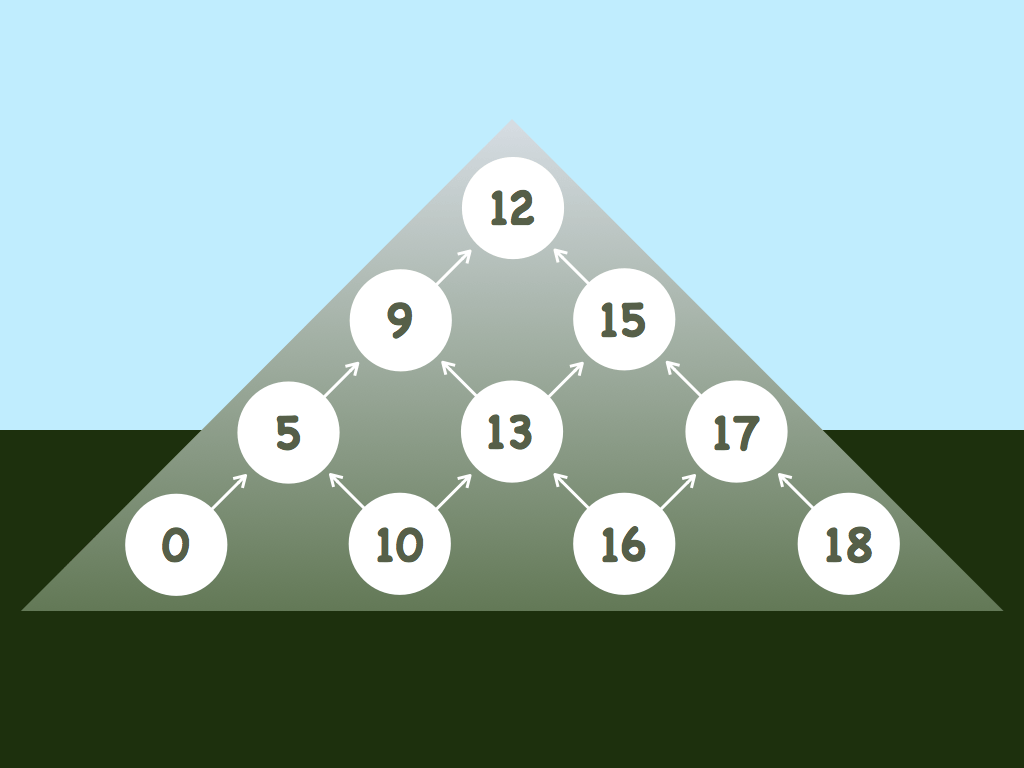
Cardboard Snowflakes is for students finding the mean of more than two integers. It is curricular for grade 6 under the Common Core State Standards.

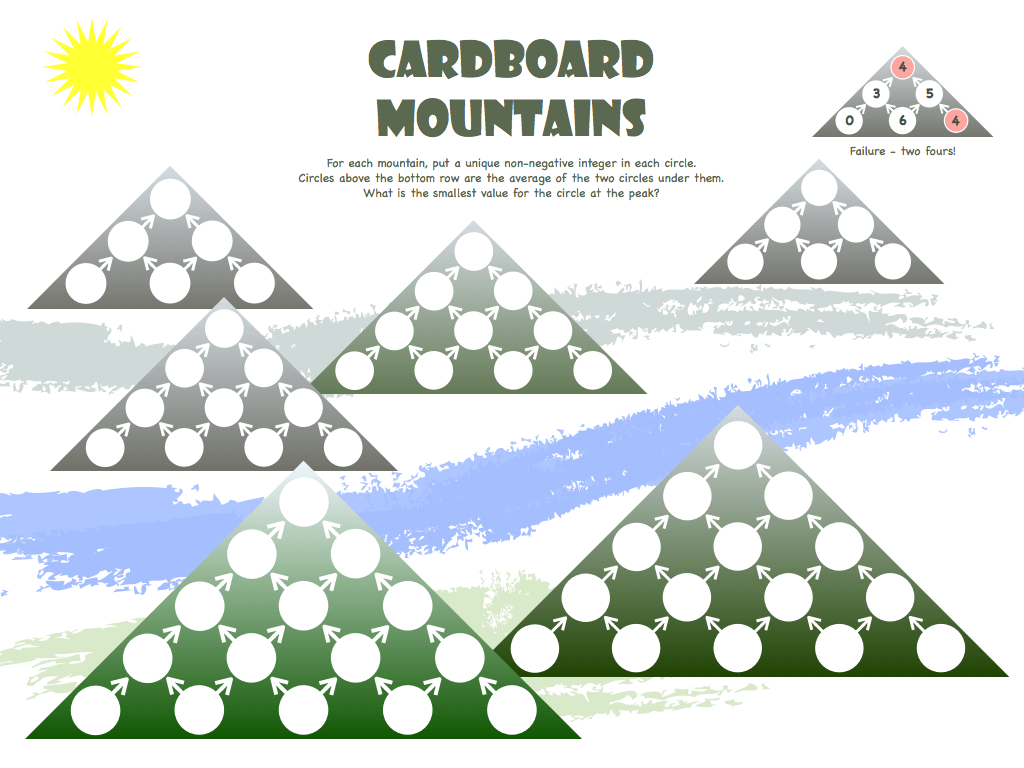
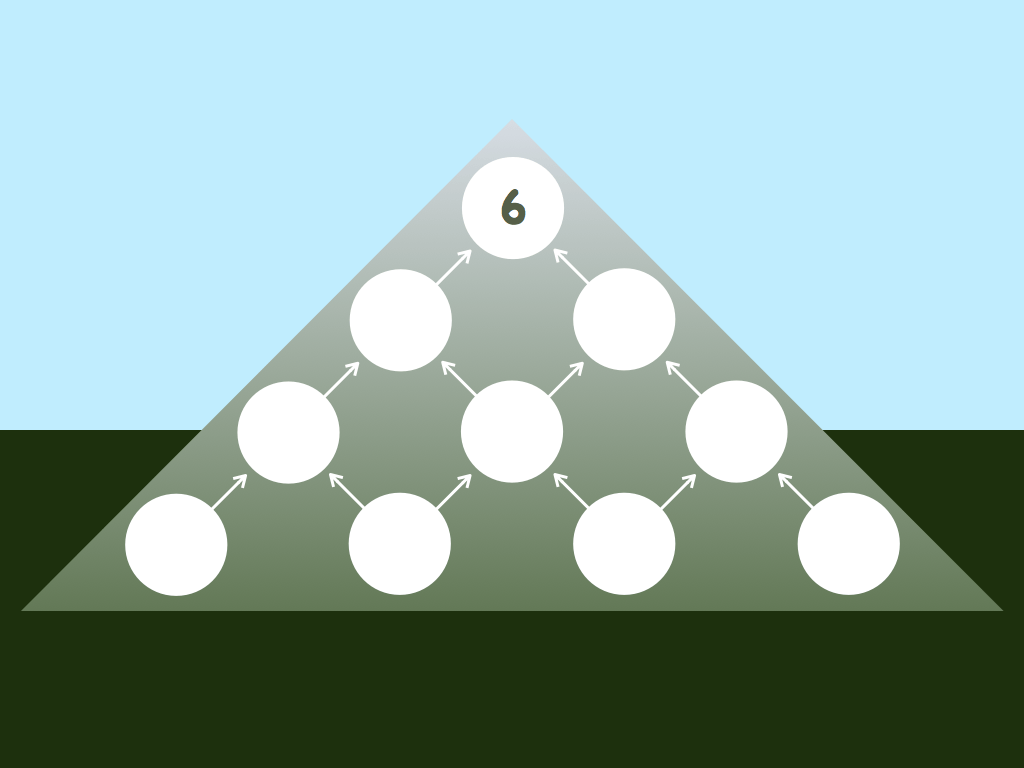
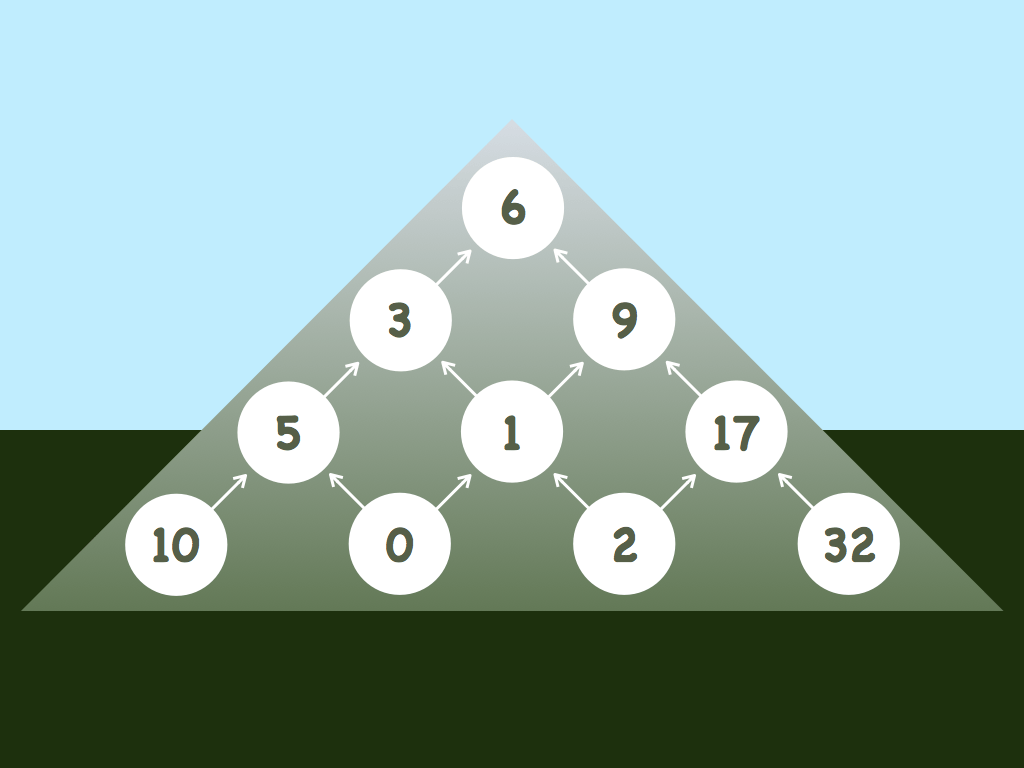
Cardboard Mountains is for students finding the mean of exactly two integers. This is appropriate for students in grade 4 – long before they can find the average of more than two integers. Four years after I published this puzzle I got an email from Henry Klaassen – a teacher at Mount Cheam Christian School in Chilliwack, BC, Canada. One of his students – Nina Kerkhoff – had just beaten what I thought was a pretty good number on top of the Cardboard Mountain of height four. The best I had found was six. She found a mountain with 5 at the summit. Wow! Instead of revealing her whole mountain I will just say that it does contain a six, but I’ll leave it to you to figure out where 😉 Congratulations Nina!

The last puzzle sheet – Cardboard Toboggan Hills is for students to explore number patterns that arise out of these challenges.

Standards for Mathematical Practice

MathPickle puzzle and game designs engage a wide spectrum of student abilities while targeting the following Standards for Mathematical Practice:

MP1 Toughen up!

Students develop grit and resiliency in the face of nasty, thorny problems. It is the most sought after skill for our students.

MP2 Think abstractly!

Students take problems and reformat them mathematically. This is helpful because mathematics lets them use powerful operations like addition.

MP3 Work together!

Students discuss their strategies to collaboratively solve a problem and identify missteps in a failed solution. Try pairing up elementary students and getting older students to work in threes.

MP4 Model reality!

Students create a model that mimics the real world. Discoveries made by manipulating the model often hint at something in the real world.

MP5 Use the right tools!

Students should use the right tools: 0-99 wall charts, graph paper, mathigon.org. etc.

MP6 Be precise!

Students learn to communicate using precise terminology. Students should not only use the precise terms of others but invent and rigorously define their own terms.

MP7 Be observant!

Students learn to identify patterns. This is one of the things that the human brain does very well. We sometimes even identify patterns that don't really exist! 😉

MP8 Be lazy!?!

Students learn to seek for shortcuts. Why would you want to add the numbers one through a hundred if you can find an easier way to do it?

(http://www.corestandards.org/Math/Practice/)

Please use MathPickle in your classrooms. If you have improvements to make, please contact me. I'll give you credit and kudos 😉 For a free poster of MathPickle's ideas on elementary math education go here.