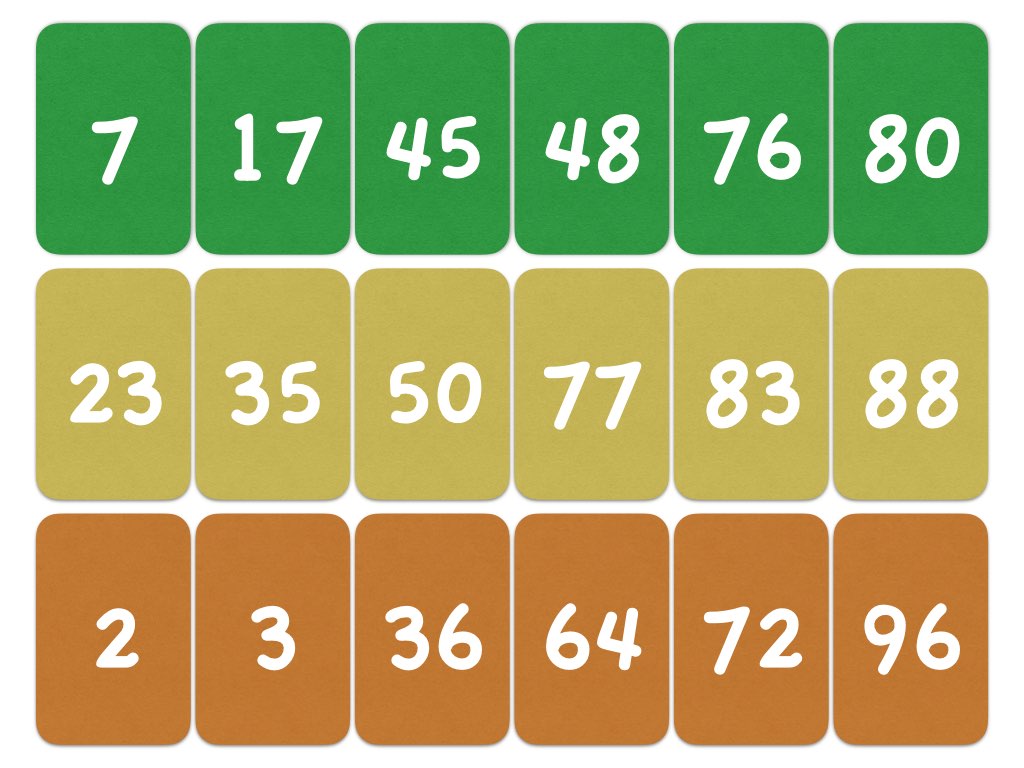
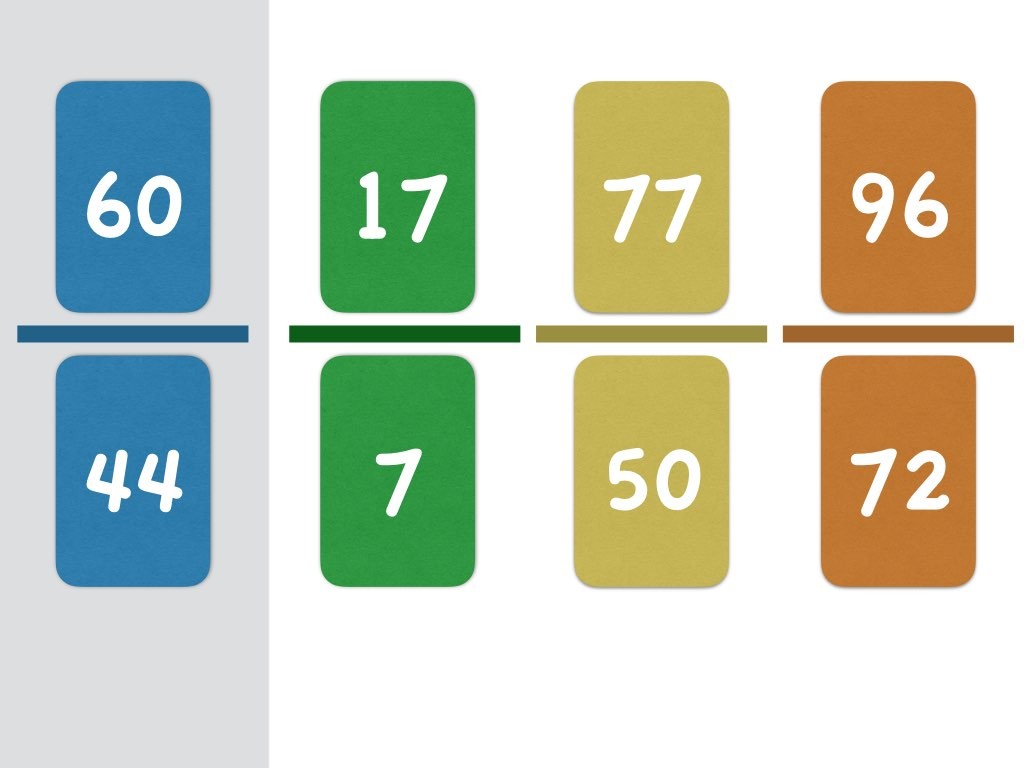
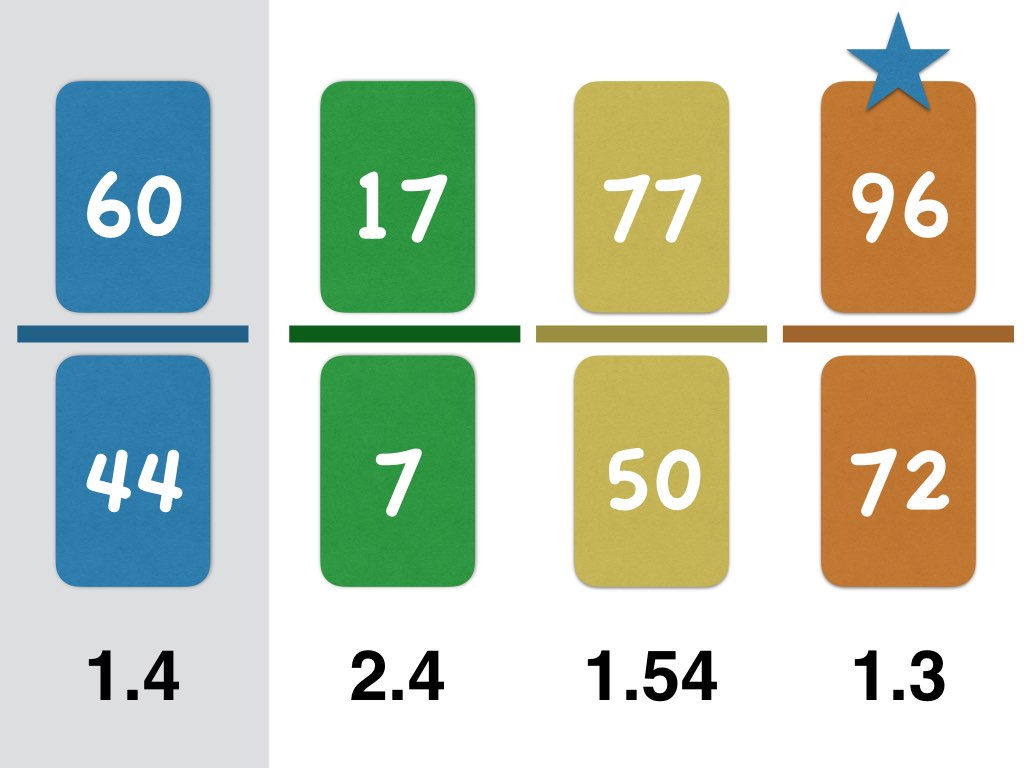
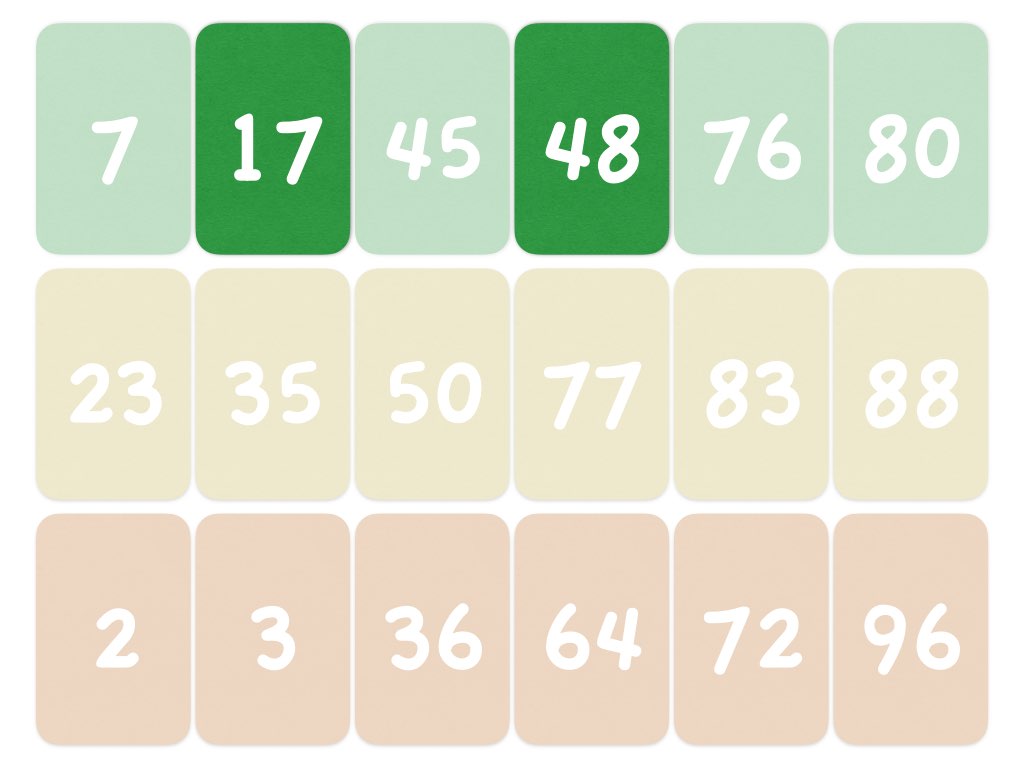
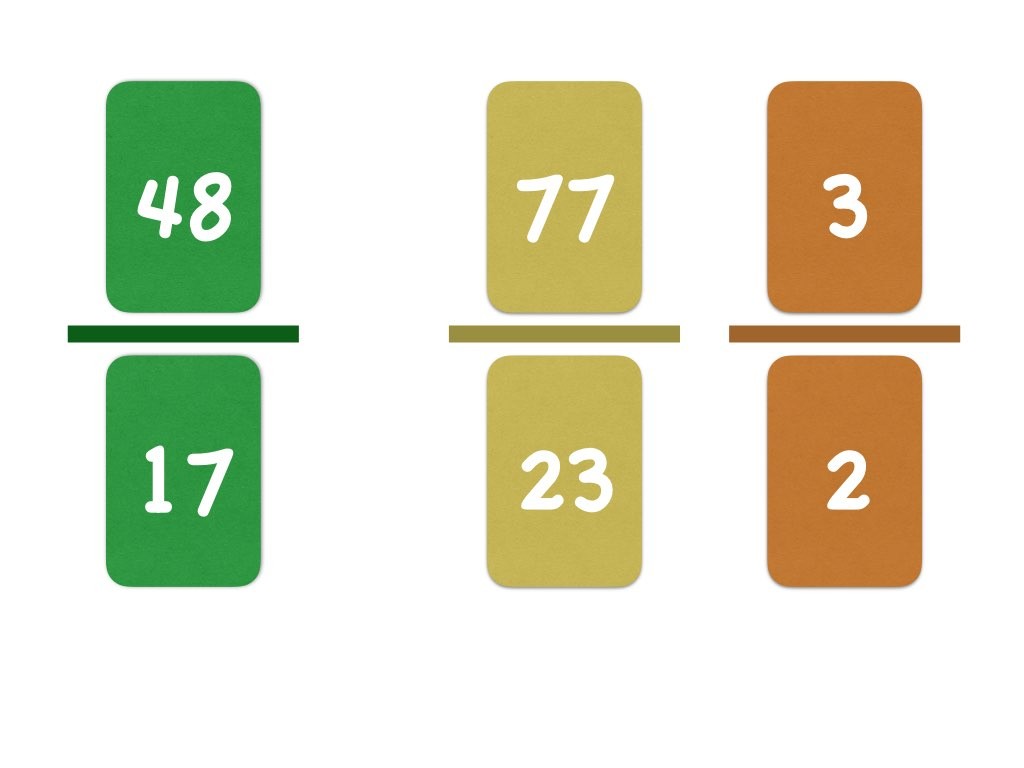
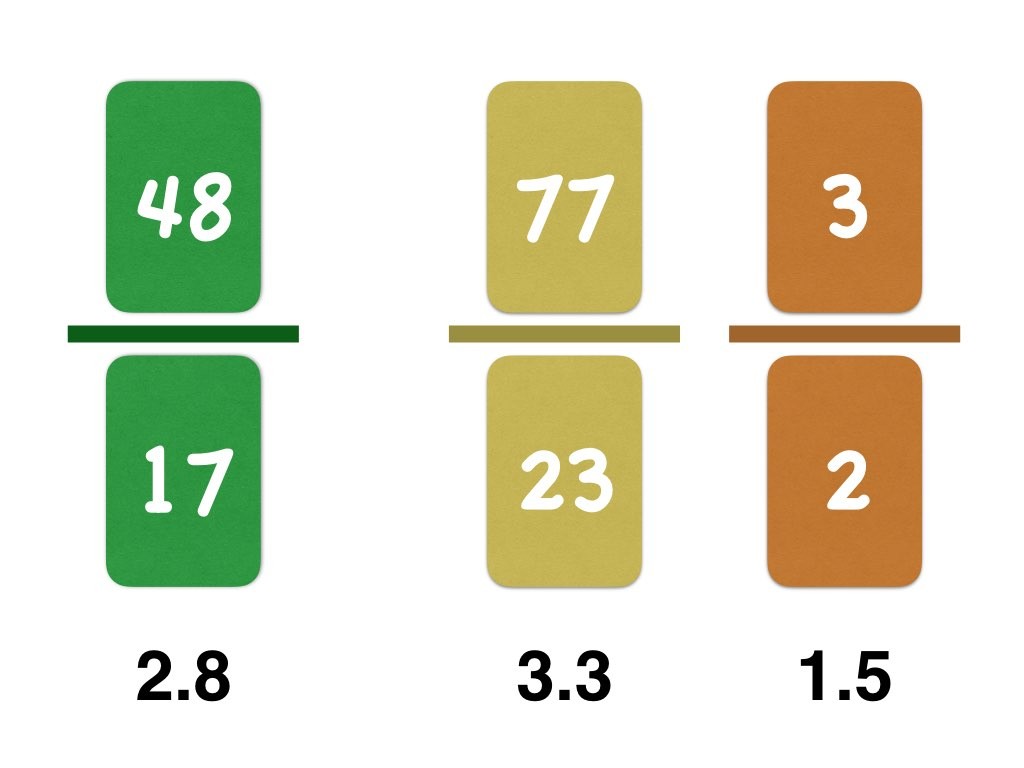
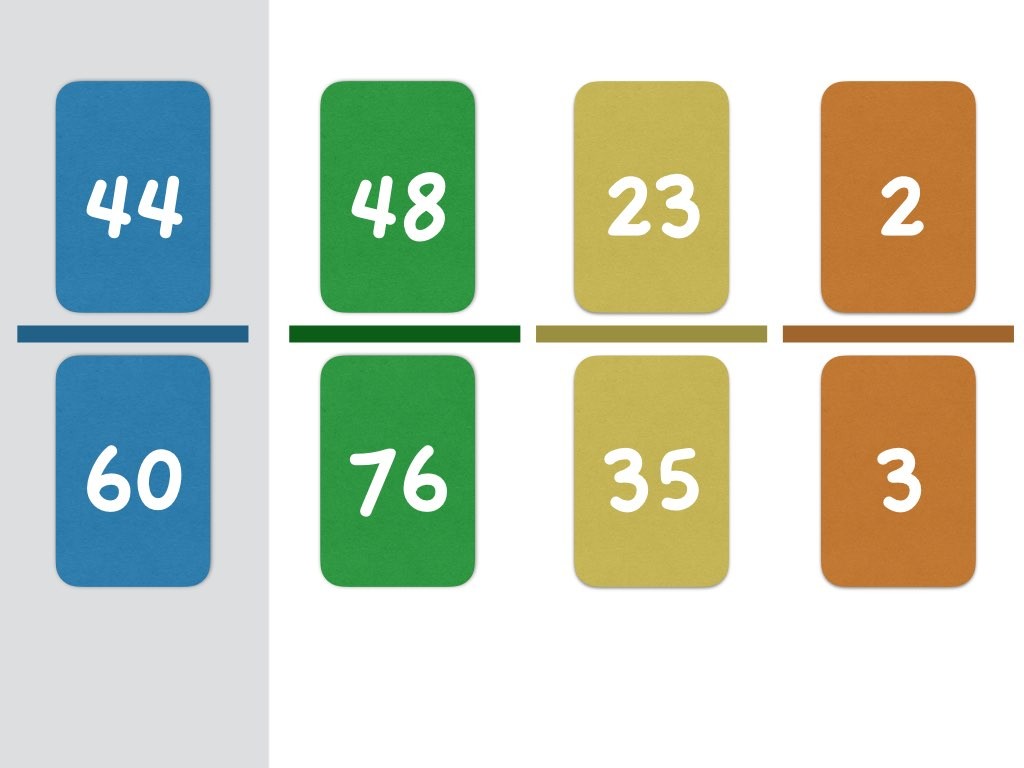
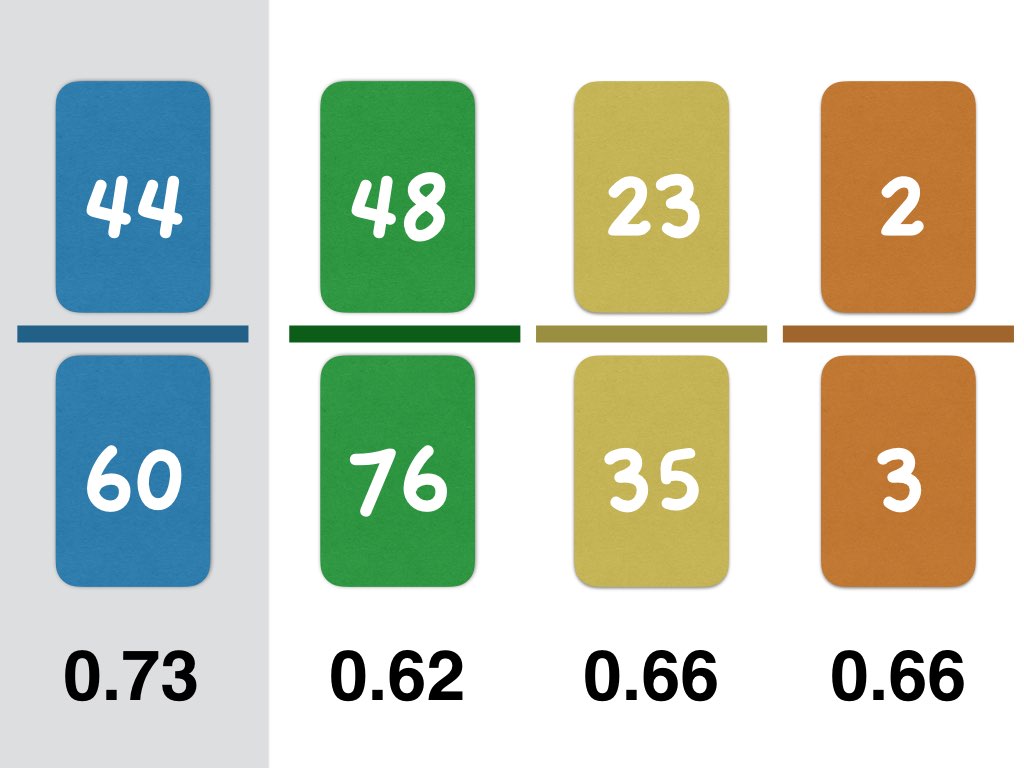
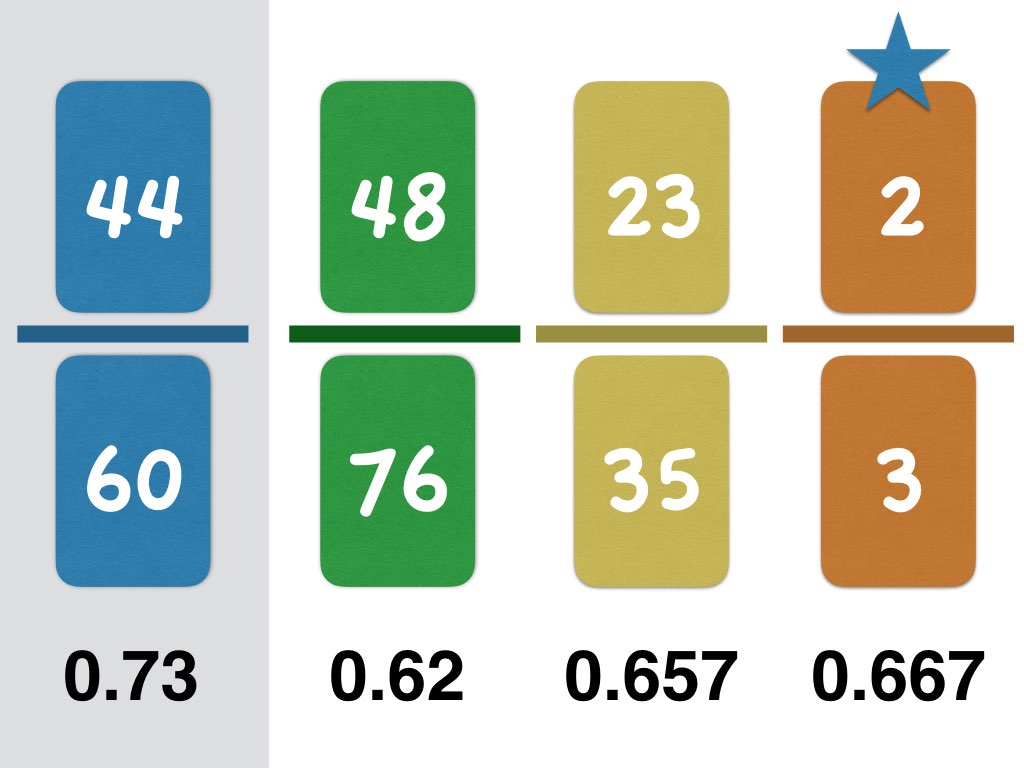
Venus Flytrap – dangerous decimals
(MathPickle, 2013)
Here is a pdf to print the cards and rules of the game. Enjoy 😉
Standards for Mathematical Practice
MathPickle puzzle and game designs engage a wide spectrum of student abilities while targeting the following Standards for Mathematical Practice:
MP1 Toughen up!
Students develop grit and resiliency in the face of nasty, thorny problems. It is the most sought after skill for our students.
MP2 Think abstractly!
Students take problems and reformat them mathematically. This is helpful because mathematics lets them use powerful operations like addition.
MP3 Work together!
Students discuss their strategies to collaboratively solve a problem and identify missteps in a failed solution. Try pairing up elementary students and getting older students to work in threes.
MP4 Model reality!
Students create a model that mimics the real world. Discoveries made by manipulating the model often hint at something in the real world.
MP5 Use the right tools!
Students should use the right tools: 0-99 wall charts, graph paper, mathigon.org. etc.
MP6 Be precise!
Students learn to communicate using precise terminology. Students should not only use the precise terms of others but invent and rigorously define their own terms.
MP7 Be observant!
Students learn to identify patterns. This is one of the things that the human brain does very well. We sometimes even identify patterns that don't really exist! 😉
MP8 Be lazy!?!
Students learn to seek for shortcuts. Why would you want to add the numbers one through a hundred if you can find an easier way to do it?
Please use MathPickle in your classrooms. If you have improvements to make, please contact me. I'll give you credit and kudos 😉 For a free poster of MathPickle's ideas on elementary math education go here.