Vidal Sassoon
1928 - 2012
Vidal Sassoon was an anti-fascist street-thug who became a mathematical sculptor of hair:
We learned to put discipline in the haircuts by using actual geometry, actual architectural shapes and bone structure. The cut had to be perfect and layered beautifully, so that when a woman shook it, it just fell back in.
Rafael Araujo
Rafael is a Venezuelan artist who celebrates the mathematical beauty of nature.
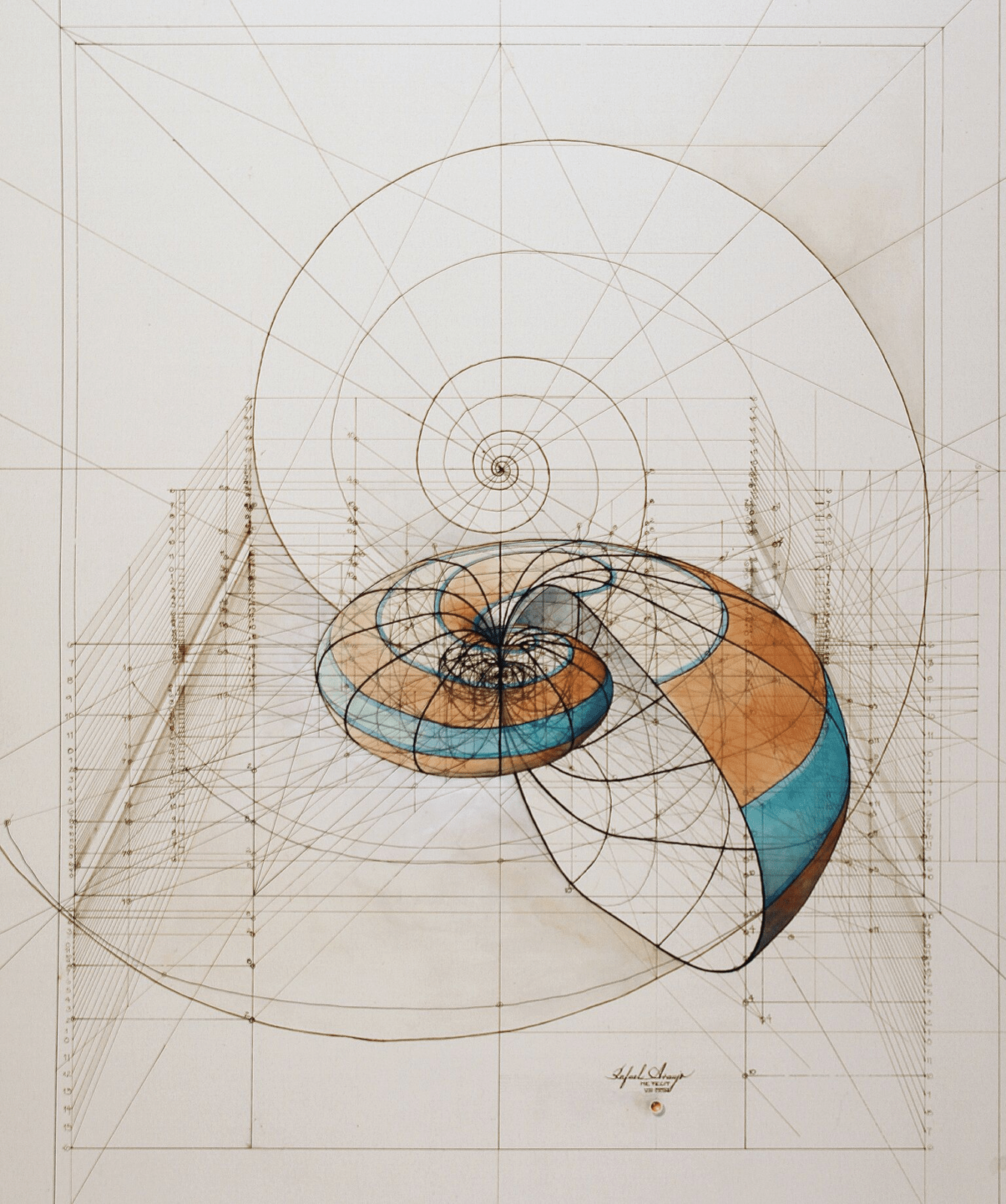
Rafael does all of his drawings by hand: http://www.rafael-araujo.com/
Colin Wright
This intensely Aussie mathematician / juggler developed the SiteSwap notation to help jugglers record and communicate their patterns. It ended up to be such a powerful notation that new juggling patterns were discovered. SiteSwap should be in ALL math curricula worldwide. It is beautiful and engaging for children. If school children learn how to juggle – well that’s just a fun side effect 😉
Here is a great lecture by Colin and here are Colin’s notes on SiteSwap. Here is a cool Brazilian video showing a top juggler using SiteSwap.
I had the pleasure of rooming with Colin and Henry Segerman (also featured on this list) at the Gathering for Gardner in 2010. Inspired people!
Photo by Ben Sparks.
M. C. Escher
1898 - 1972
M. C. Escher’s playful treatment of tiling patterns and illusions makes him a favourite artist of mathematicians.
Robert Lang
1961 -
Jorge Luis Borges
1899 - 1986
Jorge Luis Borges should be a favourite writer among mathematicians. His short stories highlight twisted worlds that are logically consistent. These two recommendations take 10 minutes to read:
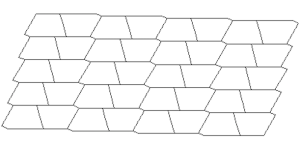
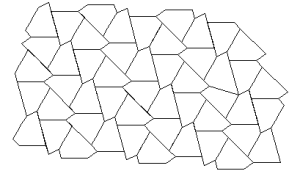
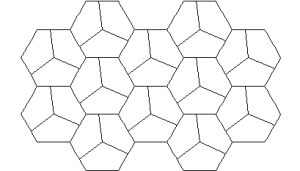
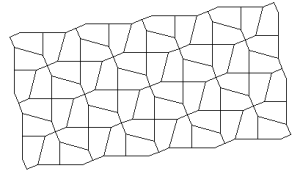
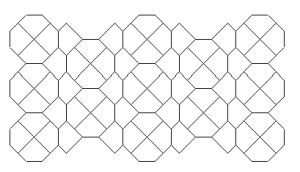
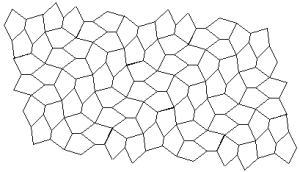
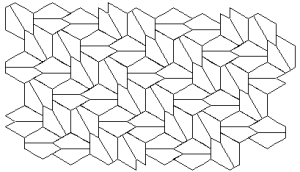
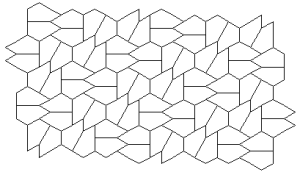
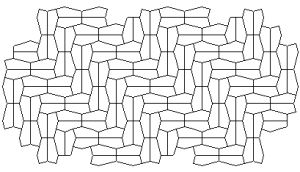
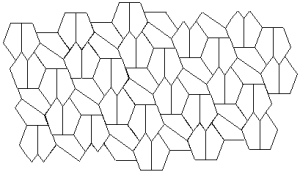
Marjorie Rice
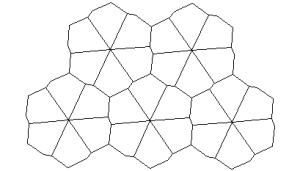
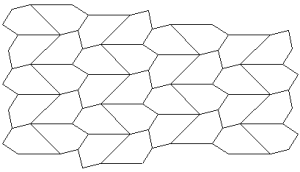
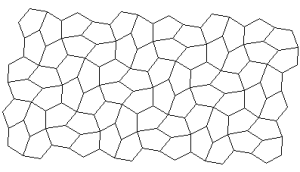
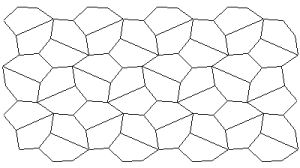
You should neither overestimate the worth of a university degree nor underestimate those with limited credentials. High school graduate, Marjorie Rice, discovered four new classes of pentagonal tiling patterns between 1975 and 1976 after mathematician R. B. Kershner announced that he had found the last of them in 1968. All the pentagons must be identical. Here are the 14 that have been discovered so far:
K. Reinhardt, 1918
K. Reinhardt, 1918
K. Reinhardt, 1918
K. Reinhardt, 1918
K. Reinhardt, 1918
R. B. Kershner, 1968
R. B. Kershner, 1968
R. B. Kershner, 1968
R. James, 1975
Marjorie Rice, 1976-77
Marjorie Rice, 1976-77
Marjorie Rice, 1976-77
Marjorie Rice, 1976-77
R Stein in 1985
You can see a discussion here. How many classes of pentagonal tiling patterns still remain to be discovered? Can someone tell me if ANY upper bound has been established?
PS. I put Marjorie in with the artists, but she probably belongs with the mathematicians.
Tomoko Fuse
1951 -
Tomoko is a master of modular origami. Her beautiful designs belong somewhere in every child’s experience of mathematics. There are many instructional videos on YouTube if you want to try to fold some of your own, but the ones pictured below are advanced.
Photo above by Prof. Finn
Dave Brill, Nick Robinson, Tomoko Fuse, and the late Michael Shall in Sheffield, 1989
Bathsheba Grossman
I admit it – I am a HUGE fan of Bathsheba Grossman’s work.
When MathPickle hits big time, all its corporate office doorknobs will be Bathsheba Grossman doorknobs.
You’ve got to admit that’s much more interesting than the gold dreams of Midas.
Here is an excellent interview with Bathsheba together with snapshots of her art.
Henry Segerman
Henry Segerman is a gifted man at the juncture of mathematics and art. His art has the minimalist beauty that mathematicians find irresistible 😉 Here is his web site: http://www.segerman.org/
I had the joy to meet Henry at Gathering for Gardner in 2010 in Atlanta.
Scott Kim
Ambigrams are playful creations at the intersection of calligraphy and symmetry operations. Your students could learn about mirror, translational and rotational symmetry through simple geometric shapes, but they should also learn about symmetry through M. C. Escher’s art or Scott Kim’s calligraphic ambigrams:
