
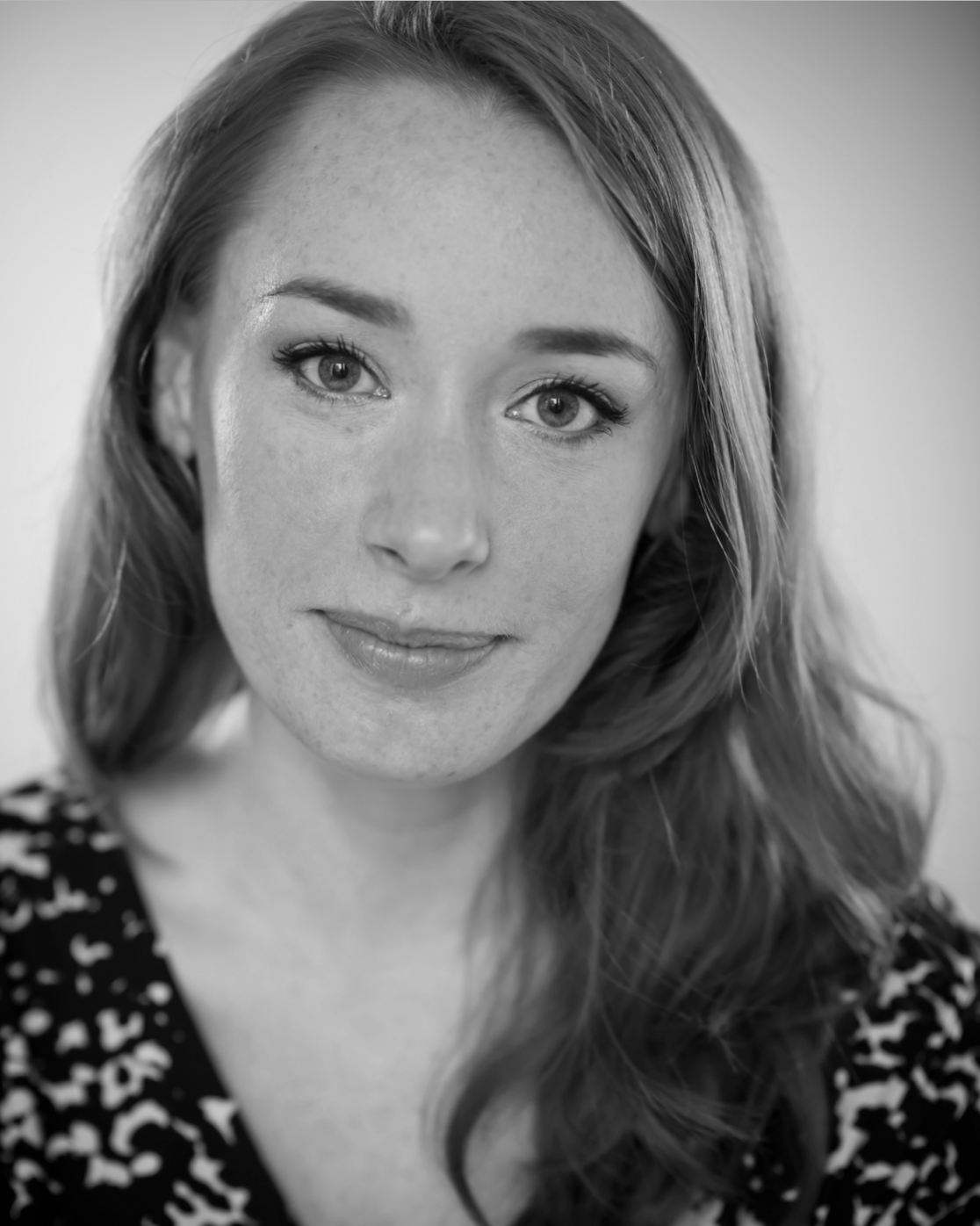
Hannah Fry
A brilliant and charismatic mathematician – Hannah Fry is a popular speaker and author. Her book “The Mathematics of Love” is typical of her down-to-earth way of communicating what the public wants to hear. She is a frequent guest on Numberphile and in 2018 hosted a prescient documentary on the next pandemic.

Maryam Mirzakhani
1977 -
Fast forward 20 years. In 2014, Maryam became Iran’s first winner of highest award in mathematics – the Fields Medal. She’s also the first woman mathematician so honoured. The win caused controversy in Iran when the head-uncovered picture below was tweeted by President Hassan Rouhani congratulating Maryam.

Luckily, the Iranian media found an old photo of her with a hijab and photoshopped the politically correct picture above which was published in Iran.
Many of Iran’s top mathematicians choose to leave the country. This is irritating for a country that obviously does a good job in identifying and nurturing its talented youth – both male and female.
A sad coincidence – In Calgary I share office-space with the brother of one of those who died in the 1998 bus crash which killed many of Iran’s top young mathematicians. Maryam survived the crash.

Richard Kenneth Guy
1916 -
Richard is author of “Unsolved Problems in Number Theory” and therefore the single most influential person in the development of MathPickle. He’s Professor Emeritus in the math department at the University of Calgary.
My desite has been to pursue mathematics, mainly in the selfish was of just enjoying it on my own, but also wanting to pass this enjoyment on to other people, particularly as I get older and feel that at least I owe something for the terrific privilege that I’ve had of being able to live, all the time doing what I wanted to do.
His life is inspirational for its breadth and depth of passions – the big three being mountaineering, mathematics, and his wife, Louise, who died at aged 94 in 2010.
James Tanton (also featured on this list) came to visit Calgary in 2013 and Richard invited us over for a meal. Our melon was cut in slices, our chicken cordon-blue succulent. Approaching 100, Richard is something! Listen to him at age three when his parents asked him eagerly how his first day had been in kindergarten:
It was alright, but the teacher doesn’t know much. She asked me what shape the world was and all sorts of things that I thought she would have known.”
Richard retired in 1982 at age 65. Of course, he didn’t retire – you can knock on his door any day, and there he is wrapped up in mathematics:
I didn’t retire, they just stopped paying me. I was quite happy to retire. I knew that I could go on doing what I wanted to do.
I thoroughly recommend the Alpine Canada book which celebrates the life of this great human being. Click here.
Photo by Thane Plambeck

Lothar Collatz
1910 - 1990
In 1937 Lothar posed the great problem which mathematicians now refer to as the Collatz conjecture: Starting at any positive integer iteratively divide by 2 if it is even – or multiply by 3 and add one if it is odd. This is done again and again. The Collatz conjecture is that you will always get to 1. It is essential for every child learning multiplication to be exposed to this unsolved problem.
YouTube video: https://youtu.be/R4oINmqHXVY
*The problem also requires division by 2, but students should learn the problem when they are learning to multiply. MathPickle introduces it in combination with the easy-to-solve analogous problem where odd numbers get multiplied by three and one is subtracted from the product.

Kelly Miller
1863 - 1939

Sofia Kovalevskaya
1850 - 1891
In 1874 Sofia became the first woman to receive a doctorate in mathematics after escaping a conservative Russia through a pretend marriage. Did it help her secure a lucrative career in a university? Read of her turbulent life here.

Julia Robinson
1919-1985
The first woman president of the American Mathematical Society, Julia was instrumental in proving Hilbert’s tenth problem unsolvable.
A Julia Robinson Mathematics Festival is a fantastic way to get your school community involved in collaborative mathematics. MathPickle helped put on the first Julia Robinson Math Festival in Canada on March 1st, 2015, and the first one in China on May 30th, 2015.

Tadashi Tokieda
All of these activities should urgently be developed for the K-12 classroom. If the mathematics is too tough – that’s okay – it is Tadashi’s playful attitude of asking questions that is absolutely inspiring!
Of the several people in the world that I have yet to meet, Tadashi is top of the list and if anyone wants to establish the equivalent of a Nobel prize in mathematics education – Tadashi would be an excellent first recipient 😉
(Update February 2016 – I had the joy of spending an hour and a half with Tadashi at the math coffee room in Stanford.)

John Forbes Nash, Jr.
1928 – 2015
John Nash was the mathematician who developed game theory. He is best known to adult audiences through the movie “A Beautiful Mind.” He created the board game Hex, in which players take turns filling a hex in an attempt to link opposite sides. This game is a superb for young children because of its simple rules, and because it can be played on game boards of different sizes. However, just because it is easy to learn does not mean that it is easy to master!

Paul Erdős
1913 - 1996
Paul Erdős was one of the greatest mathematicians of the 20th century. He roamed the world, with no fixed address – moving from house to house as the guest of other mathematicians – generating living and travelling expenses by giving lectures. Most mathematicians deteriorate as they grow into middle age, but Paul was contributing mightily till his death at a mathematics conference. He is author or co-author of more mathematical papers than anybody else in history.
Here is a question he asked that kindergarten students can understand, but remains unsolved:
How many little squares of the same size can fit into a big square of a certain size?

Leo Moser
1921-1970
Leo Moser is the first person who advocated unsolved problems being used in K-12 education. He asked many tough problems with child-like zeal:
What’s the area of the smallest house that a unit worm can live comfortably?
…meaning what shape can cover a worm no matter how he curls up?

Marcus du Sautoy
1965 -
Marcus du Sautoy is the sartorially charismatic Simonyi Professor for the Public Understanding of Science, a mathematics professor at Oxford, and one of the great popularizers of mathematics.
Photo by Niccolò Caranti

Frederik Schuh
1875 - 1966
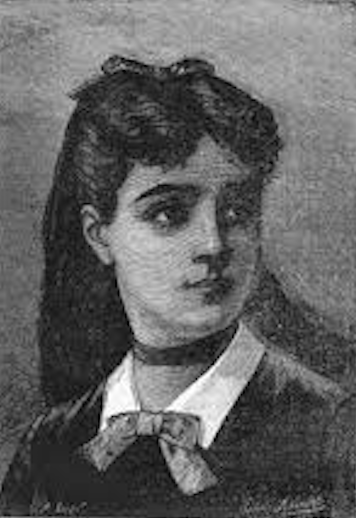
Sophie Germain
1776 – 1831

Hypatia
370 - 415

Issai Schur
1875 - 1941
Issai Schur was a quiet, naive mathematician who had very little time for religion or politics. He could never understand the Nazi preoccupation with his Jewish heritage. In his mind, he was a German – not a Jew. Ousted from his respected academic position in Germany, he ended up in Palestine where he died in poverty on his 66th birthday.
We remember him with the an unsolved problem which he asked in 1916 – Mathematicians call it Schur’s Sum-Free Partition Problem, but despite the big words, this problem belongs in front of every classroom learning addition.
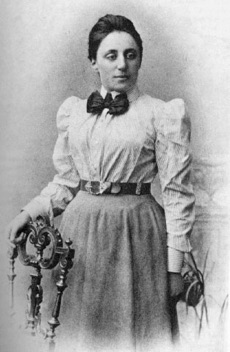
Emmy Noether
1882-1935
The University of Göttingen had a policy against women becoming professors, but Emmy was so good they had to do something. They gave her the grand title “unofficial associate professor” before stripping it away in the anti-Jewish pogroms of the early 1930s. She escaped to the United States where she helped Einstein with the general theory of relativity.

Srinivasa Ramanujan
1887 - 1920
For many mathematicians, this man shares the same sky-high pedestal with Archimedes, Newton, Gauss and Euler.
Ramanujan had no formal education in pure mathematics yet developed incredible results. His correspondence with the British mathematician G. H. Hardy are legendary. Can you imagine being an upper crust English gentleman and receiving a mathematical manuscript from the backwaters of the Indian subcontinent. Surely there would be nothing of interest.
One sequence that Ramanujan explored were the positive integers that have more factors than any smaller positive integers. For example 30 has eight factors 1, 2, 3, 5, 6, 10, 15, 30. If that is more factors than any smaller number, then 30 is a “Highly Composite Number.” Alas, 24 also has eight factors, so 30 is not included. In 1915, Ramanujan impressively found the first 102 Highly Composite Numbers with a single omission: 293,318,625,600.
MathPickle introduces Ramanujan’s Highly Composite Numbers when half the students in a class can find all the factors of 36, 40 and 42.

Ron Graham
1935 -
Ron Graham is a mathematician, and as you can see he also juggles. There is a lot of mathematics in juggling, so it is a hobby for a lot of young mathematicians. Ron Graham is a past president of the International Juggler’s Association.
One unsolved problem with Egyptian fractions (fractions with 1 as the numerator) was posed by Ron Graham in 1964 and is related to a lot of solvable challenges for students learning how to add and subtract fractions with different denominators. Here is one: Start with 17/20 of a pie. Greedily choose the largest Egyptian fraction you can. Repeat this until you’ve eaten everything.
17/20 – 1/2 = 7/20
7/20 – 1/3 = 1/60
1/60 – 1/60 = 0
Now try it with 16/20, 18/20 and 19/20. Remember to be greedy! You must always choose the largest piece.

Norman Wildberger

Lai-Sang Young
1952 -

Tatiana Ehrenfest-Afanassjewa
1876 - 1964
A Russian / Dutch mathematician who advocated against the step by step instruction of Greek geometry. She skipped over obvious proofs – telling her students that these could be re-visited later. She also loved getting her students to experiment – using clocks to talk about angles and asking how many desks could be placed against the classroom wall.
Here is an English translation of a German paper she wrote in 1931.

Gerhard Ringel
1919 - 2008
Gerhard Ringel’s twin passions were mathematics and butterflies. Upon his retirement from the University of California, Santa Cruz, he donated 5000 butterfly specimens – many of which he had reared from the egg.
His Graceful Tree Conjecture has remained unsolved since 1967, and is essential in any class learning subtraction.
To see the the problem in a real grade three classroom go here.
