Mondrian Art Puzzles
(MathPickle, 2015)
This first video with Brady Haran for Numberphile is a joy for me. It is, however, not the type of video to show a class because it will demotivate them. You never want your students to believe they are competing against computers. They will do better to believe they are creating and discovering original stuff. An elementary student’s world is small. Keep it that way 😉
After the numberphile video came out Hannes Bassen was inspired to write an academic paper on Mondrian Art Puzzles. He found optimal scores superior to the optimal scores presented in the Numberphile video! Ed Pegg has made long range predictions about the behaviour of the sequence generated by optimal scores…







Below are the record values discovered by students, teachers, mathematicians and parents. Some of these scores may drop further. The 10×10 square seems especially difficult to get a nice low value for. Perhaps a score of 9 is as low as possible. Do not show this list to your class. They should compete among themselves or with another class at your school. Anyone wishing to extend this list beyond 12×12 or those finding better solutions should email me.
Low Score for 4x4
Low Score for 5x5
Low Score for 6x6
Low Score for 7x7
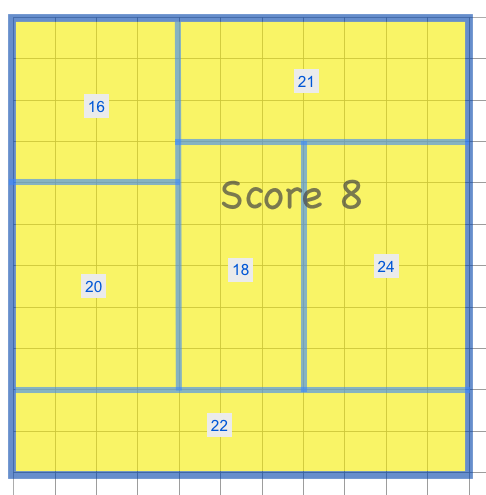
Low Score for 8x8
Low Score for 9x9
Low Score for 10x10 (Ed Pegg, 2016)
Low Score for 11x11 (Ed Pegg, 2016)
Low Score for 12x12 (Ed Pegg, 2016)
Low Score for 13x13 (Ed Pegg, 2016)
Low Score for 14x14 (Hannes Bassen, 2016)
Low Score for 15x15 (Hannes Bassen, 2016)
Low Score for 16x16 (Hannes Bassen, 2016)
Low Score for 17x17 (Ed Pegg, 2016)
Low Score for 18x18 (Hannes Bassen, 2016)
Low Score for 19x19 (Hannes Bassen, 2016)
Low Score for 20x20 (Hannes Bassen, 2016)
Low Score for 21x21 (Ed Pegg, 2016)
Low Score for 22x22 (Ed Pegg, 2016)
Low Score for 23x23 (Ed Pegg, 2016)
Low Score for 24x24 (Ed Pegg, 2016)
Low Score for 25x25 (Hannes Bassen, 2016)
Low Score for 26x26 (Hannes Bassen, 2016)
Low Score for 27x27 (Hannes Bassen, 2016)
Low Score for 28x28 (Hannes Bassen, 2016)
Low Score for 29x29 (Hannes Bassen, 2016)
Low Score for 30x30 (Hannes Bassen, 2016)
Low Score for 32x32 (Hannes Bassen, 2016)










Alison Hansel’s class has produced a most joyous celebration of Mondrian Art Puzzles below and left 😉
They are using a 10 by 10 grid. I’m not sure which the best result is, but it might be the one on the second rightmost column and the second row from the bottom.
Thank you all!



Standards for Mathematical Practice
MathPickle puzzle and game designs engage a wide spectrum of student abilities while targeting the following Standards for Mathematical Practice:
MP1 Toughen up!
Students develop grit and resiliency in the face of nasty, thorny problems. It is the most sought after skill for our students.
MP2 Think abstractly!
Students take problems and reformat them mathematically. This is helpful because mathematics lets them use powerful operations like addition.
MP3 Work together!
Students discuss their strategies to collaboratively solve a problem and identify missteps in a failed solution. Try pairing up elementary students and getting older students to work in threes.
MP4 Model reality!
Students create a model that mimics the real world. Discoveries made by manipulating the model often hint at something in the real world.
MP5 Use the right tools!
Students should use the right tools: 0-99 wall charts, graph paper, mathigon.org. etc.
MP6 Be precise!
Students learn to communicate using precise terminology. Students should not only use the precise terms of others but invent and rigorously define their own terms.
MP7 Be observant!
Students learn to identify patterns. This is one of the things that the human brain does very well. We sometimes even identify patterns that don't really exist! 😉
MP8 Be lazy!?!
Students learn to seek for shortcuts. Why would you want to add the numbers one through a hundred if you can find an easier way to do it?
Please use MathPickle in your classrooms. If you have improvements to make, please contact me. I'll give you credit and kudos 😉 For a free poster of MathPickle's ideas on elementary math education go here.