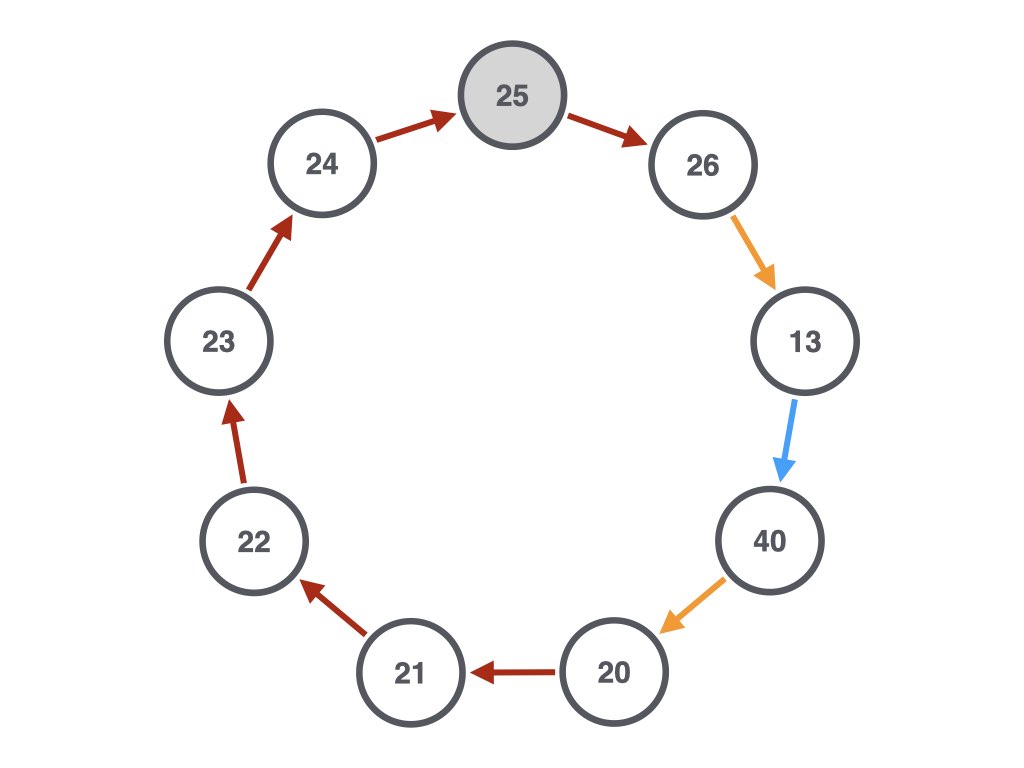
Minimal trips around the Collatz Galaxy

(MathPickle, 2025)

What’s going on in this loop? We are going to present it to students as a mystery to be discovered. The solution above is a failure. Whenever you are telling a classroom of students that they failed, you are removing the stigma of failure. Have fun with it. Don’t give itsy-bitsy fails, give them EPIC FAILS!!!

Download the puzzlesheet here.

Why is the attempt above wrong? Well, first, I’ll show you part of the solution for 25. You can try to finish it off, or you can just scroll down and you’ll see the completed solution:

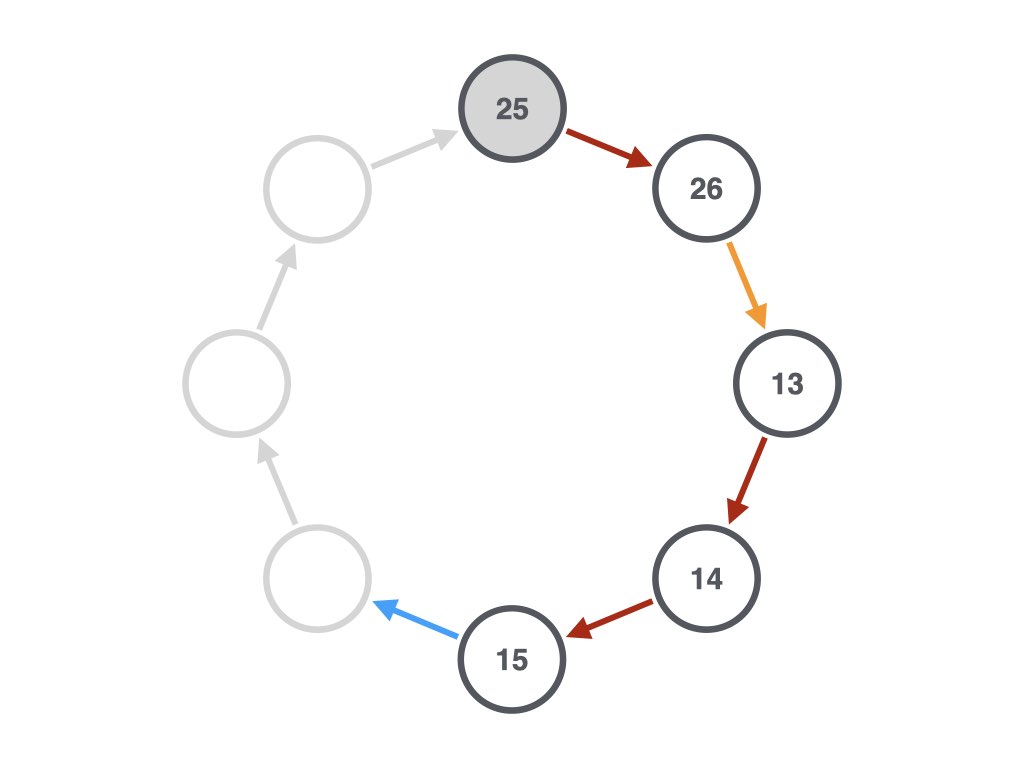
the complete solution for 25:

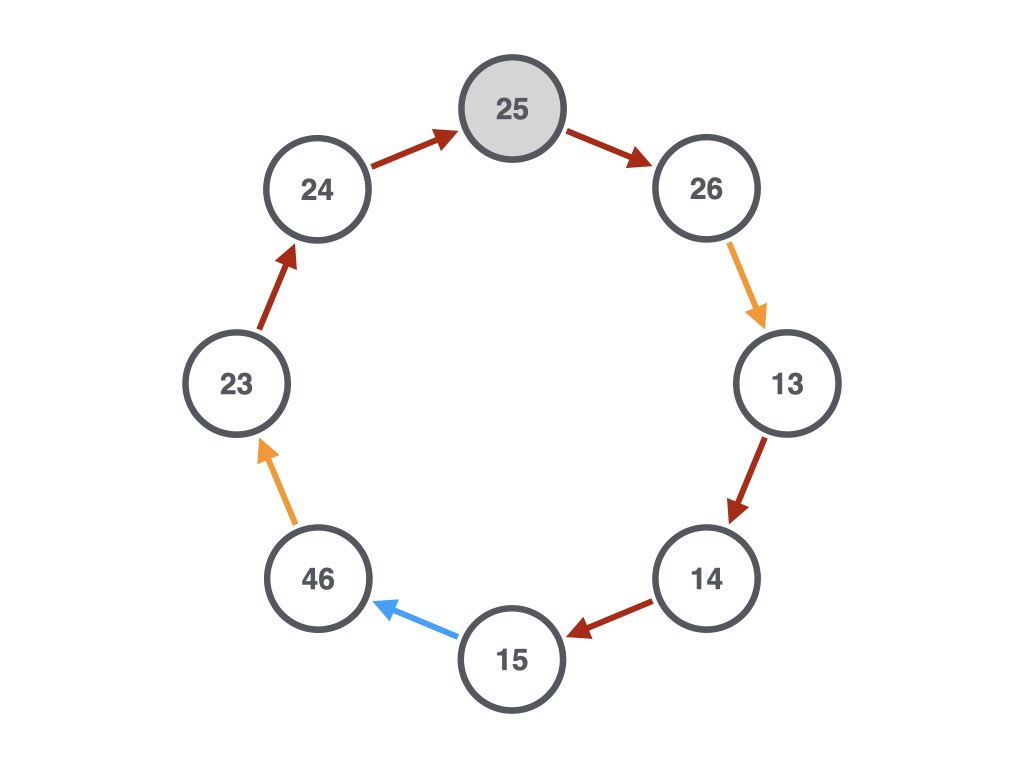
The rules are: if a number is even, you can use a yellow arrow to divide it by 2. If it is odd, you can use a blue arrow to multiply it by 3 and add 1. You can always use a red arrow to add 1.

That’s true for both the wrong solution and the correct solution for 25. What additional thing was I trying to do? I failed with the first loop of size 9, because there was a smaller loop that worked for 25. 

For any starting number what is the smallest loop? 

Now that you understand what we are trying to do, how do we introduce this to kids? 

1) Ask one child for an integer 5-10. (Do not have hands raised. You do not want to know what your extroverted, gifted students think. You want to know how all your students think.)

2) Ask another child to choose an arrow. If the number is even and they choose yellow, draw a yellow arrow and divide the number by 2. If the number is odd, have fun giving the child an EPIC FAIL. “You chose yellow? How could you suggest that! Somebody else, please! Give me a better colour!” Remember, the kids have no idea about the rules for the puzzle, so this is all in fun. 😉

The same if the child chose blue, but the number is even. Give them a fun EPIC FAIL!

3) Go around the circle until they connect, or you run out of space. Don’t do more than seven or eight arrows… If they go beyond this, give the whole class a fail and tell them that their objective is to get back to the beginning. Erase everything and try again. Never erase just one arrow and have them choose another. Remember, an EPIC FAIL is more engaging than a little mini fail.

4) The students should give their ideas about what the different arrows are doing. They still have no idea that they are trying to use the smallest number of arrows possible.

Now it is time to hand out the puzzlesheet below. You’ll find a double-sided pdf here. The back side is very light so as not to detract from the beautiful main page, especially if you are using thin paper. 

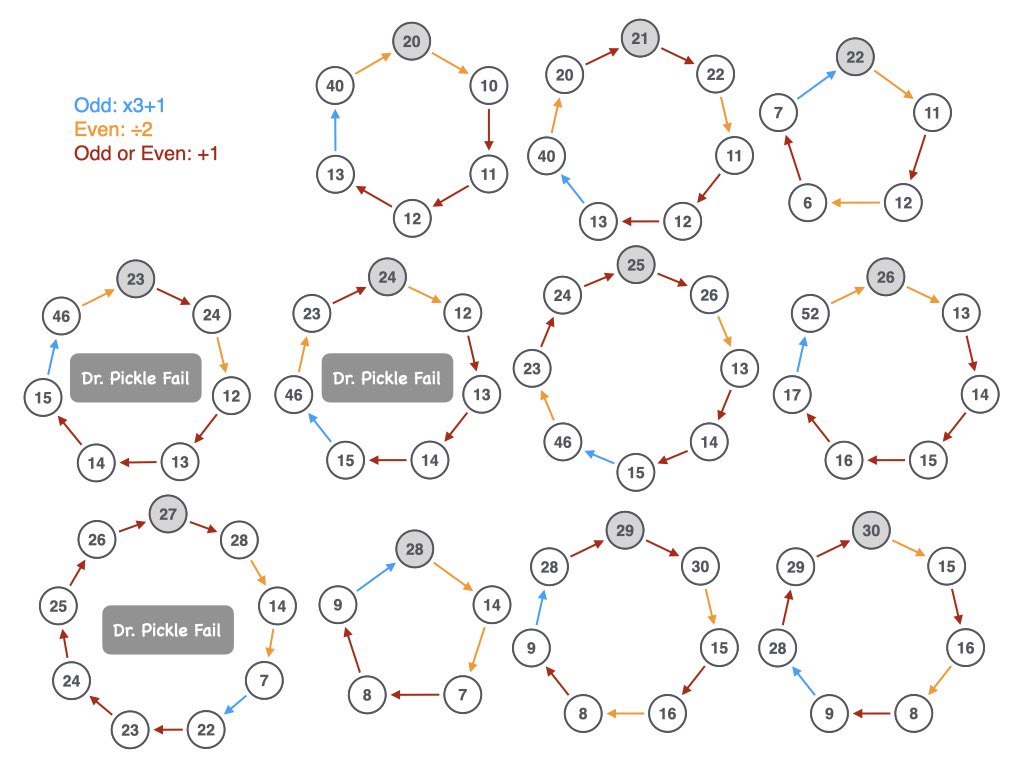
Why did Dr. Pickle fail? All the colours look right. Do not expect kids to find the answer. After a while of giving their ideas, you can tell them that we are trying to find the smallest loops that contain each integer. Dr. Pickle filed at 27 because you don’t need 9 steps; you can do it in 8.

Flip the page over and try to find a way around using the minimal number of steps. I didn’t solve the bottom three, but a computer scientist proved that these were minimal. If you choose bigger numbers, even a computer scientist will struggle. 

After students have struggled with some of the numbers on the back, you can establish a leaderboard where students from different classes compete to find the smallest loops containing specific numbers. The answer will not be found in the back of any text book. Instead, students just compete with one another to find the smallest loops.

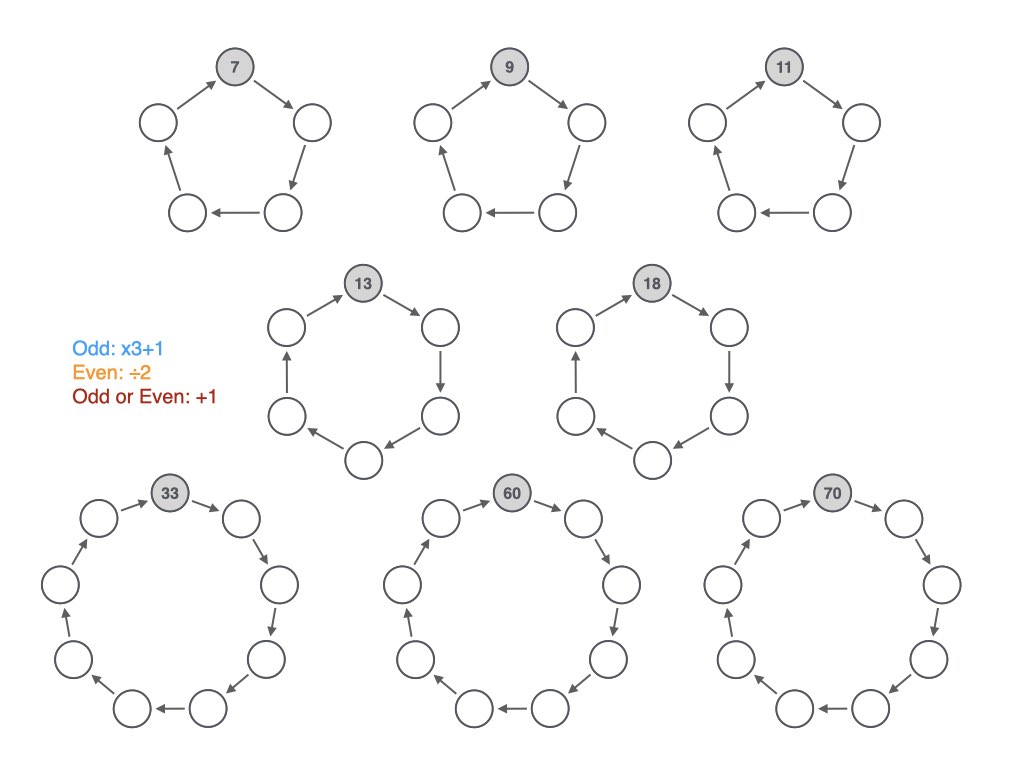
I’ve solved the upper two rows, but not 33, 60 and 70 on the bottom rows. We know that they can be solved with 9 arrows.

A blooper!

To avoid a similar fate, make sure you keep your numbers small in the classroom! Ask your students to choose a number between 5-10. If the number gets too big – pretend you misunderstood the colour! Or ask a student to secretly choose a colour and then pretend to mind-read to get the answer you want. Students love this silliness, but it’s silliness with a pedagogic purpose!

Mathematicians and eager students can get more information on this puzzle by looking at the Online Encyclopedia for Integer Sequences: OEIS A384327