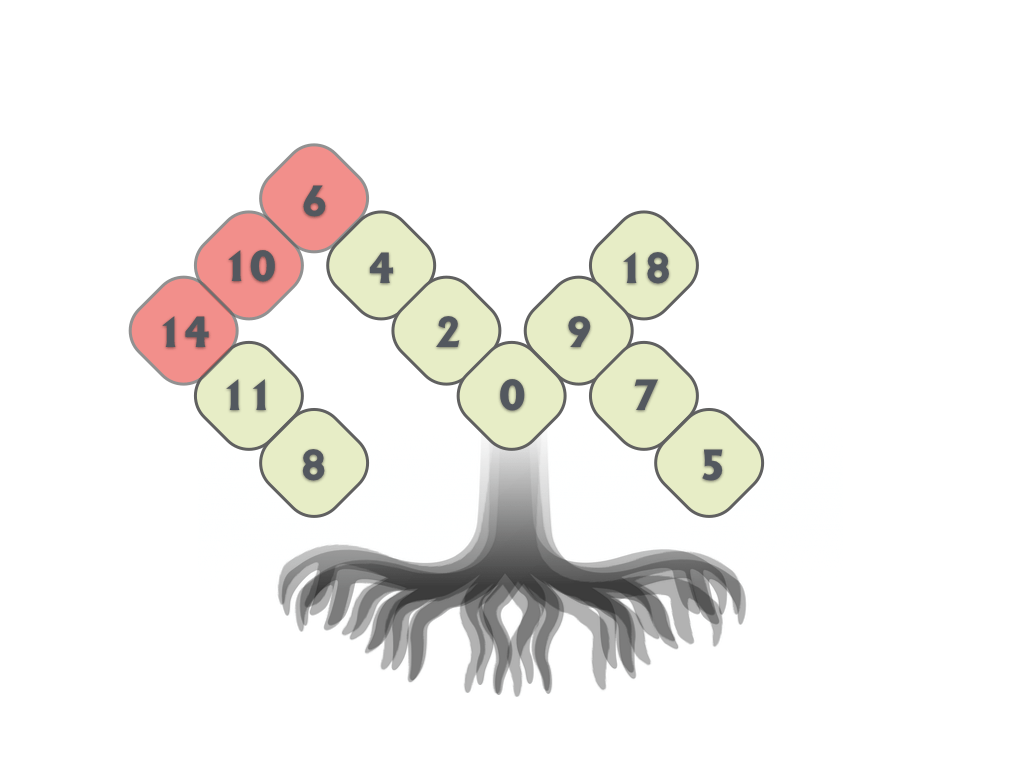
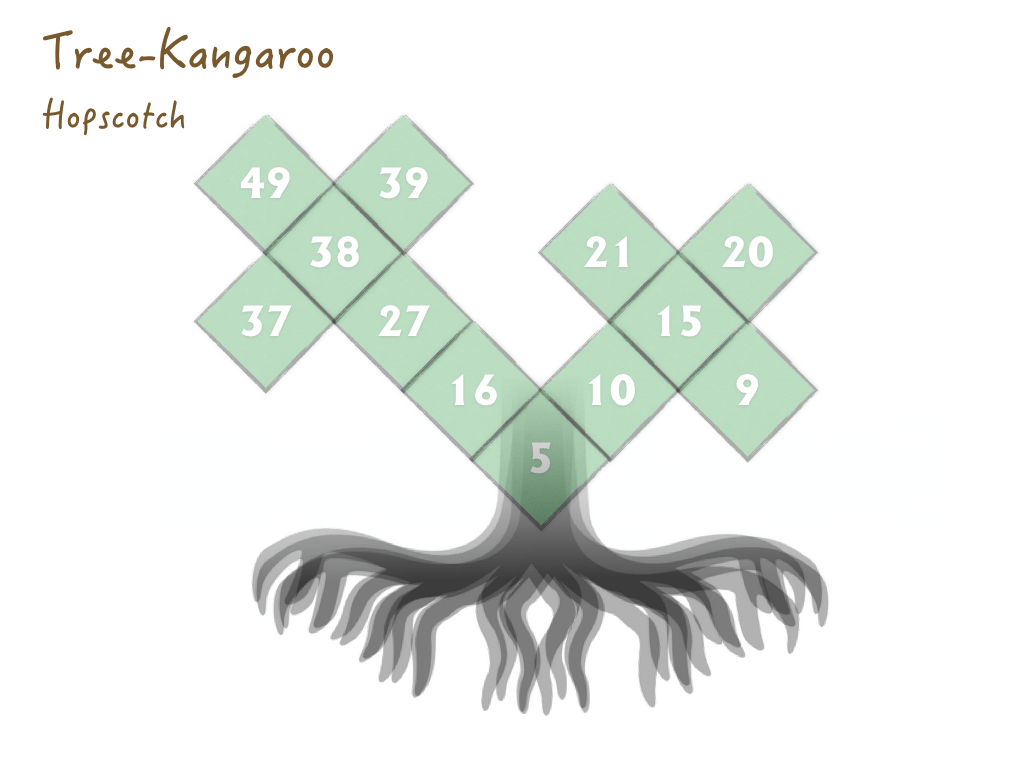
Tree Kangaroo Hopscotch (skip counting)

I did not even know of Tree Kangaroos – less so their secret ritual of arboreal hopscotch 😉

“Mammals of Australia”, Vol. II Plate 50 by John Gould (1804-1881)

When kangaroos skip count up a branch the numbers increase. Let one of them start on the right branch – skip counting by 4…

The numbers must be non-negative integers.

Next another tree kangaroo chooses a different branch…

Here they are skip counting by seven. Let’s choose the big left branch and skip count by 3…

Oh no! Here they have failed. Why?

No two numbers can be the same. This mistake probably meant the poor tree kangaroo responsible fell off the tree.

We failed in that last try.

Here is another tree…

Skip counting by 5s…

The objective is to fill the tree with different non-negative integers… with the largest integer as small as possible. Here we have scored 25… or have we?

Can you spot where the tree kangaroos failed?

Drats – it is another failure – this time because we failed to skip count on one branch. 4-7-11 isn’t skip counting by 3s or 4s.

Here the kangaroos have scored 18… or did they make another mistake?

Oops – they forgot to skip-count UP on this branch. Remember that the integers increase as you skip-count up a branch.

This is successful, but the score of 49 is much too high.

Remember: Your score is equal to the highest number in your tree. Lower is better.

Download printable pdf puzzles here.

Tree Kangaroo Hopscotch

(MathPickle, 2016)

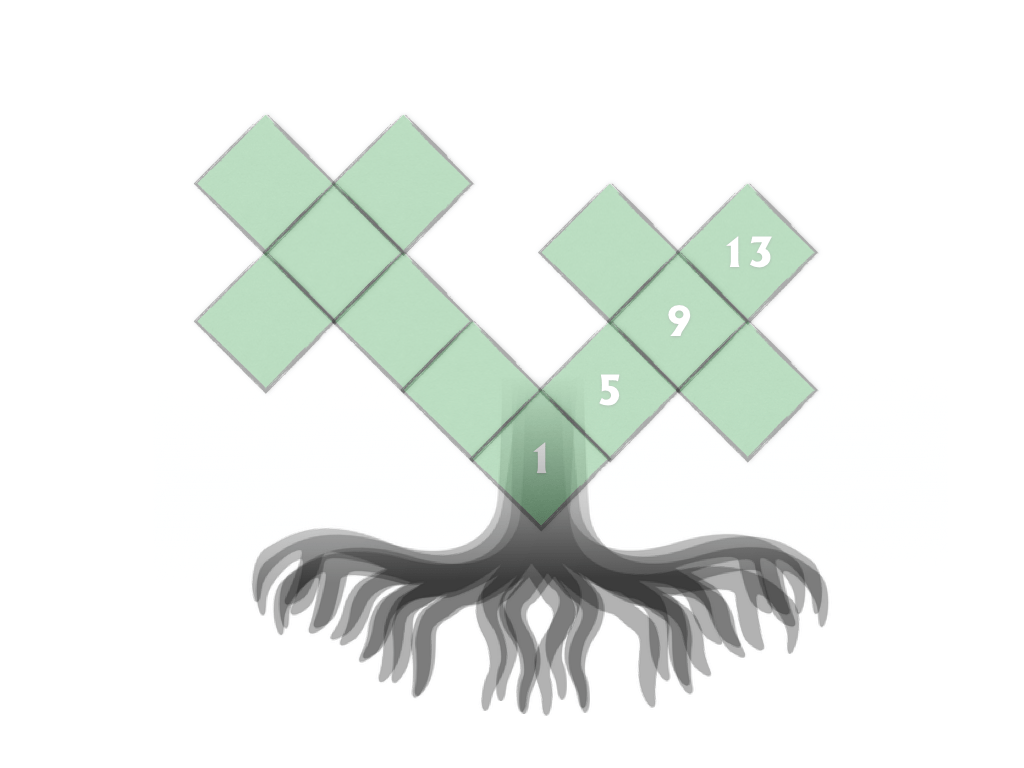
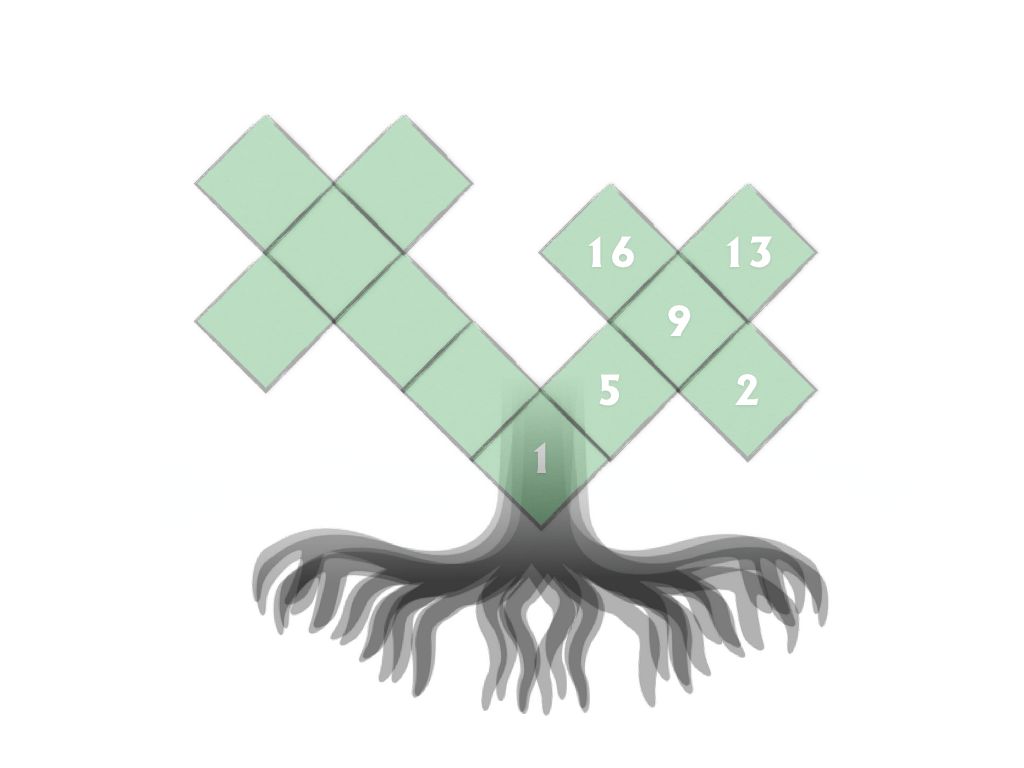
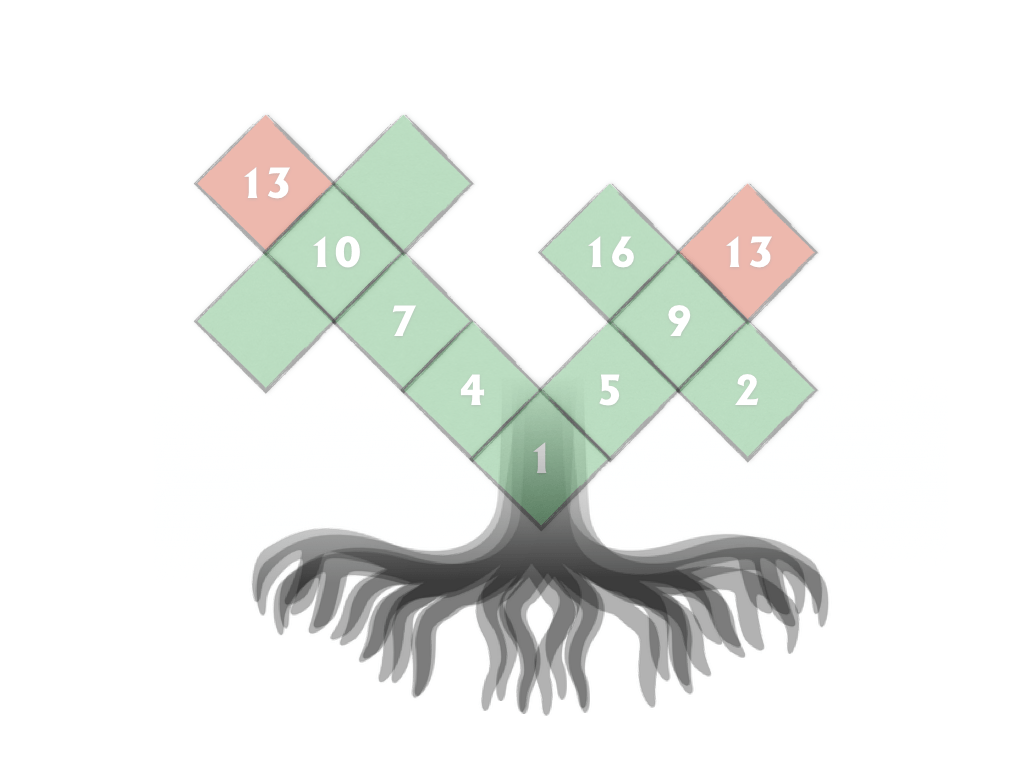
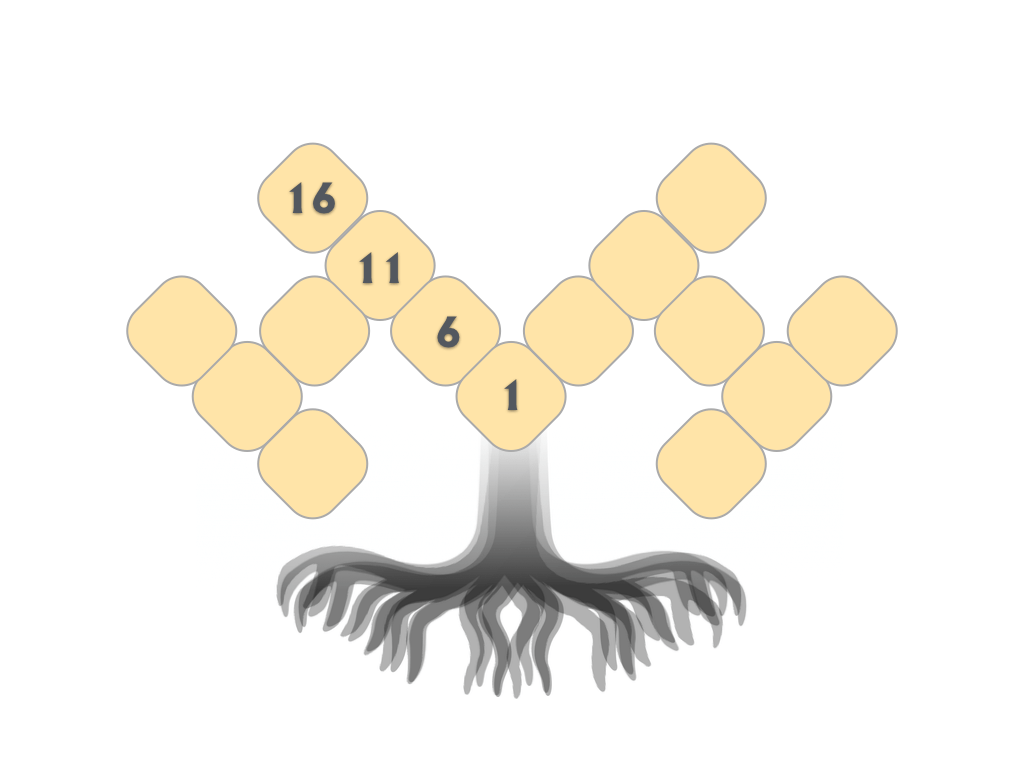
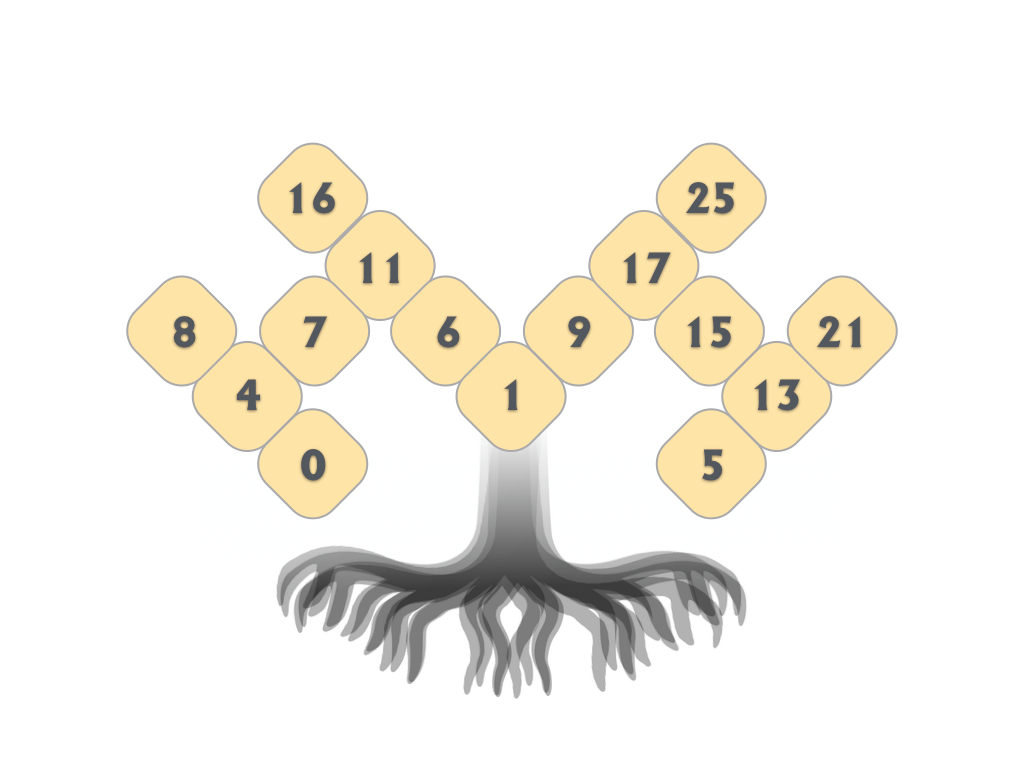
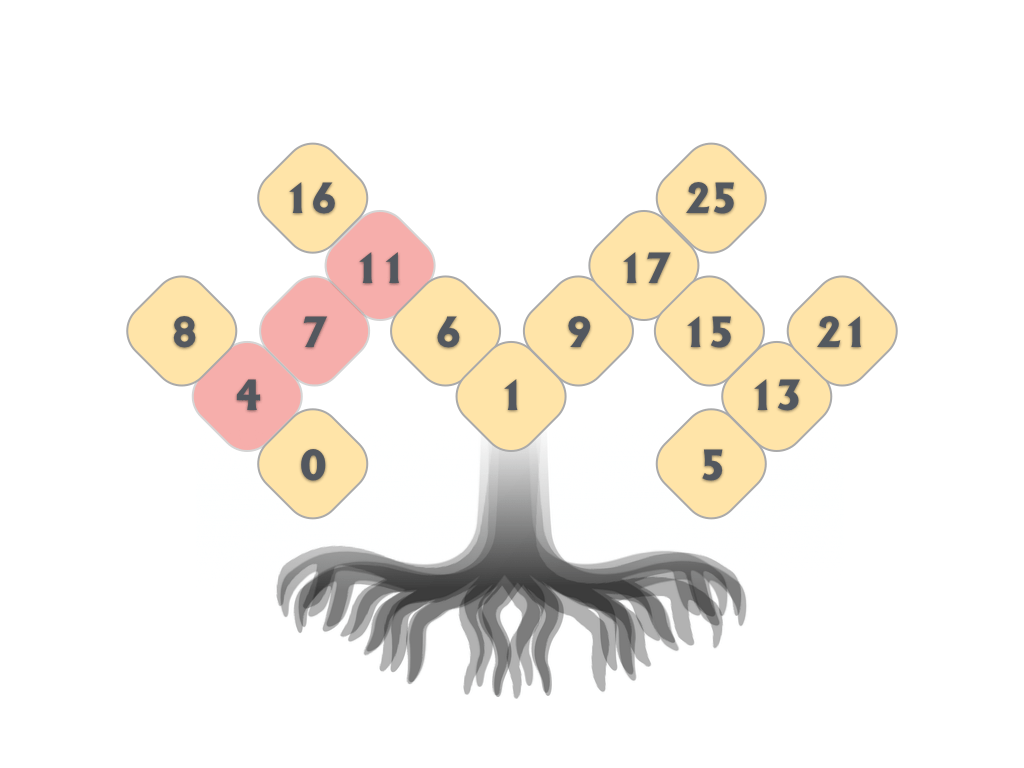
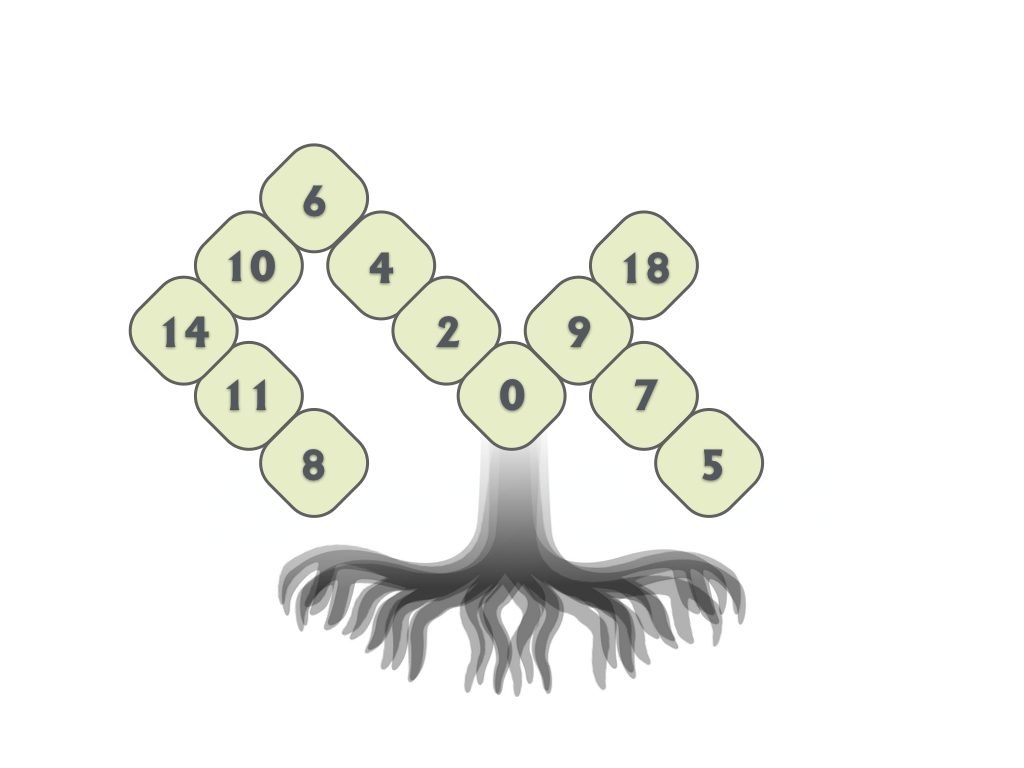
Tree Kangaroo hop scotch are difficult little optimization challenges that insist students skip count. What makes them so fiendishly difficult is that the skip counts intersect and that no number can be duplicated.

Download printable and projectable puzzle-sheets here.

Standards for Mathematical Practice

MathPickle puzzle and game designs engage a wide spectrum of student abilities while targeting the following Standards for Mathematical Practice:

MP1 Toughen up!

Students develop grit and resiliency in the face of nasty, thorny problems. It is the most sought after skill for our students.

MP2 Think abstractly!

Students take problems and reformat them mathematically. This is helpful because mathematics lets them use powerful operations like addition.

MP3 Work together!

Students discuss their strategies to collaboratively solve a problem and identify missteps in a failed solution. Try pairing up elementary students and getting older students to work in threes.

MP4 Model reality!

Students create a model that mimics the real world. Discoveries made by manipulating the model often hint at something in the real world.

MP5 Use the right tools!

Students should use the right tools: 0-99 wall charts, graph paper, mathigon.org. etc.

MP6 Be precise!

Students learn to communicate using precise terminology. Students should not only use the precise terms of others but invent and rigorously define their own terms.

MP7 Be observant!

Students learn to identify patterns. This is one of the things that the human brain does very well. We sometimes even identify patterns that don't really exist! 😉

MP8 Be lazy!?!

Students learn to seek for shortcuts. Why would you want to add the numbers one through a hundred if you can find an easier way to do it?

(http://www.corestandards.org/Math/Practice/)

Please use MathPickle in your classrooms. If you have improvements to make, please contact me. I'll give you credit and kudos 😉 For a free poster of MathPickle's ideas on elementary math education go here.