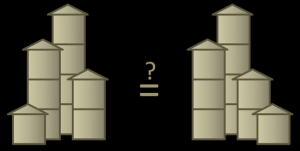This is a problem I give to my grade 1 students. The Fairy-Tale-King invites you to sit down in front of him… “design for me, a magical castle with beautiful towers.” It turns out that he has enough money to pay for ten floors and tells you to distribute these ten floors any way you like between your towers. “However”, he whispers, “None of the towers can be the same height!” For example, you could build three towers of height 4,5,1 but you could not build four towers of heights 1,3,5,1 because two towers are of height 1.
Well – that seems easy… 3,7 is a solution… 10 is a solution if you’re allowed to build just one tower… 4,3,2,1 is a solution. That’s easy – even for a grade 1 student.
Some easy problems are good problems… but the Fairy-Tale-King isn’t quite finished. He wants you to find ALL of the possible solutions. That’s not quite as easy. It requires your grade 1 students to get organized.
Just like we want to give our students exposure to problems that have no solutions, we want to expose them to problems with multiple solutions.
If they decide that these are different and that order matters, then you probably want to be prepared to take a minute and list all 24 answers and then re-focus back on the main problem.
1,2,3,4 1,2,4,3 1,3,2,4 1,3,4,2 1,4,2,3 1,4,3,2
2,1,3,4 2,1,4,3 2,3,1,4 2,3,4,1 2,4,1,3 2,4,3,1
3,1,2,4 3,1,4,2 3,2,1,4 3,2,4,1 3,4,1,2 3,4,2,1
4,1,2,3 4,1,3,2 4,2,1,3 4,2,3,1 4,3,1,2 4,3,2,1
The same is true if they come to the decision that order matters with any set of two or three towers… Just take a moment to talk about the sub-problem and then refocus back on the main problem.
1,2,7 1,7,2 2,1,7 2,7,1 7,1,2 7,2,1
How many solutions are there if they decide that order isn’t important?
I’ll just give you the answer, because I want you to understand the general idea rather than working on the specifics. There are 10.
One group might find all 10 answers and then organize them into rows based on the height of the tallest tower (left). Another group might first think how to organize their search and then decide to organize based on the number of towers (right).
I imagine that most grade 1 students cannot organize themselves sufficiently to find all 10 answers…
That’s okay. It’s the process that’s important. I would not prompt the students “there’s just one more to go – who will find it?” Rather than prompt students towards a complete solution, just let the problem stew indefinitely. Don’t think that it has to be wrapped up neatly.