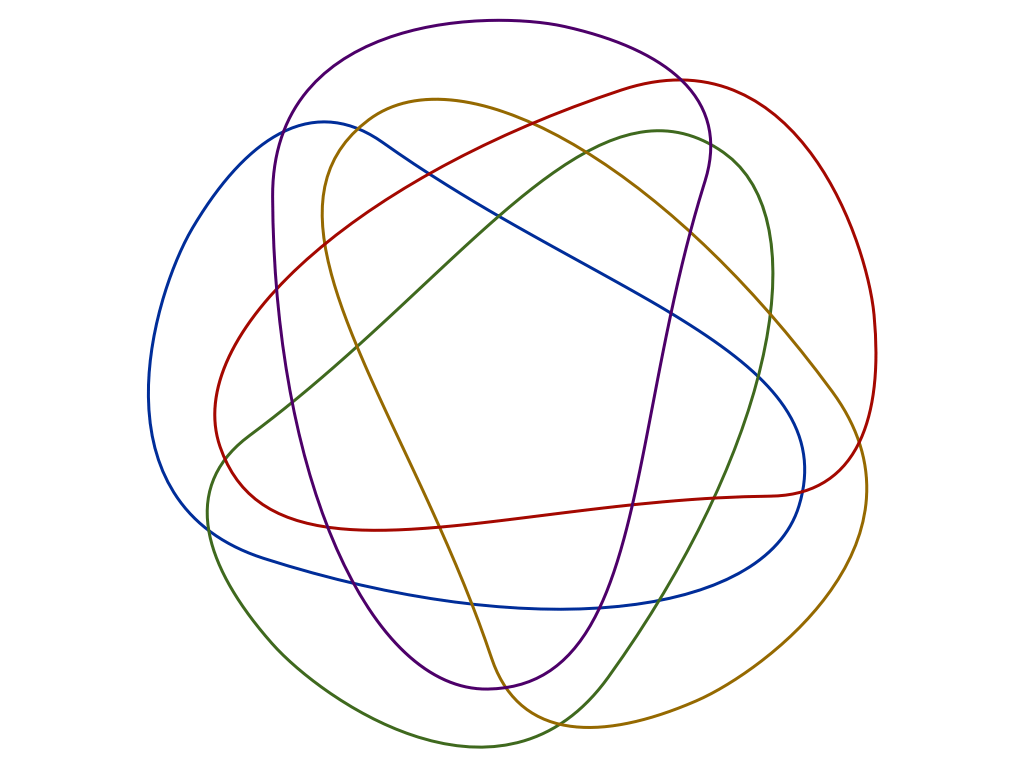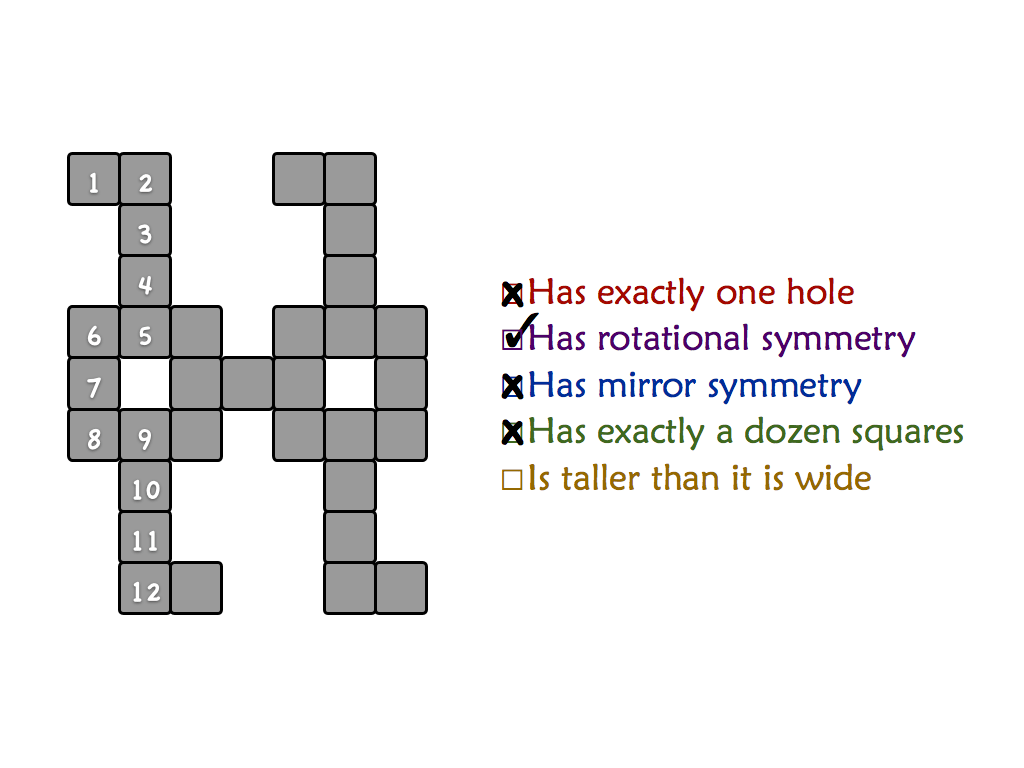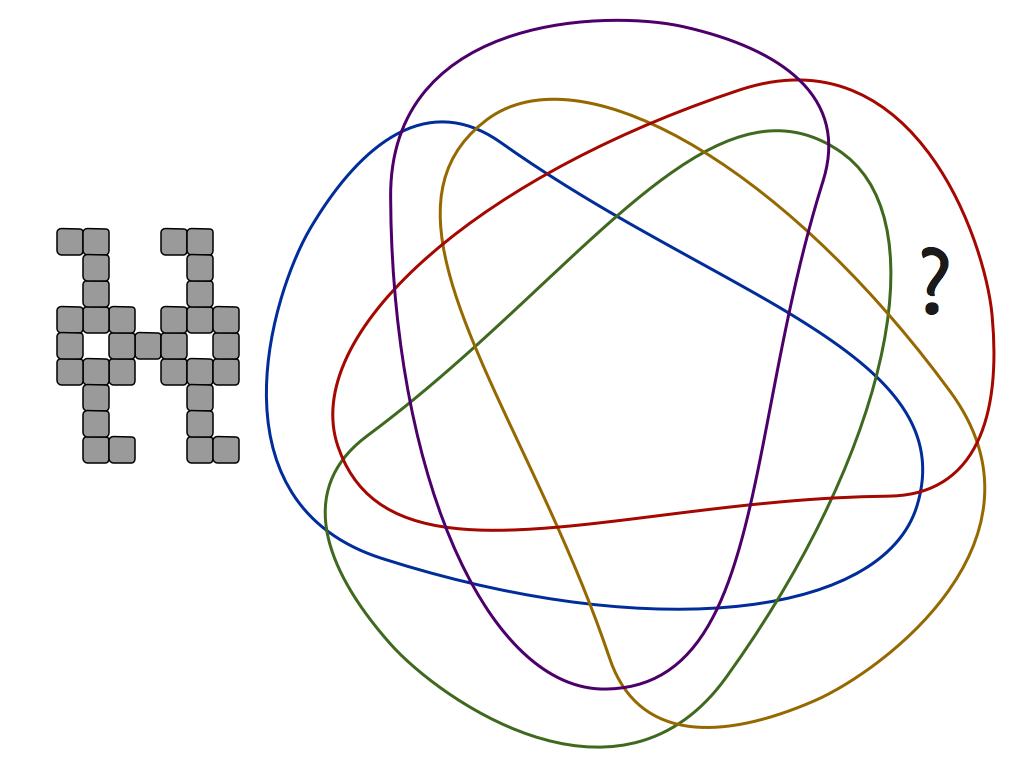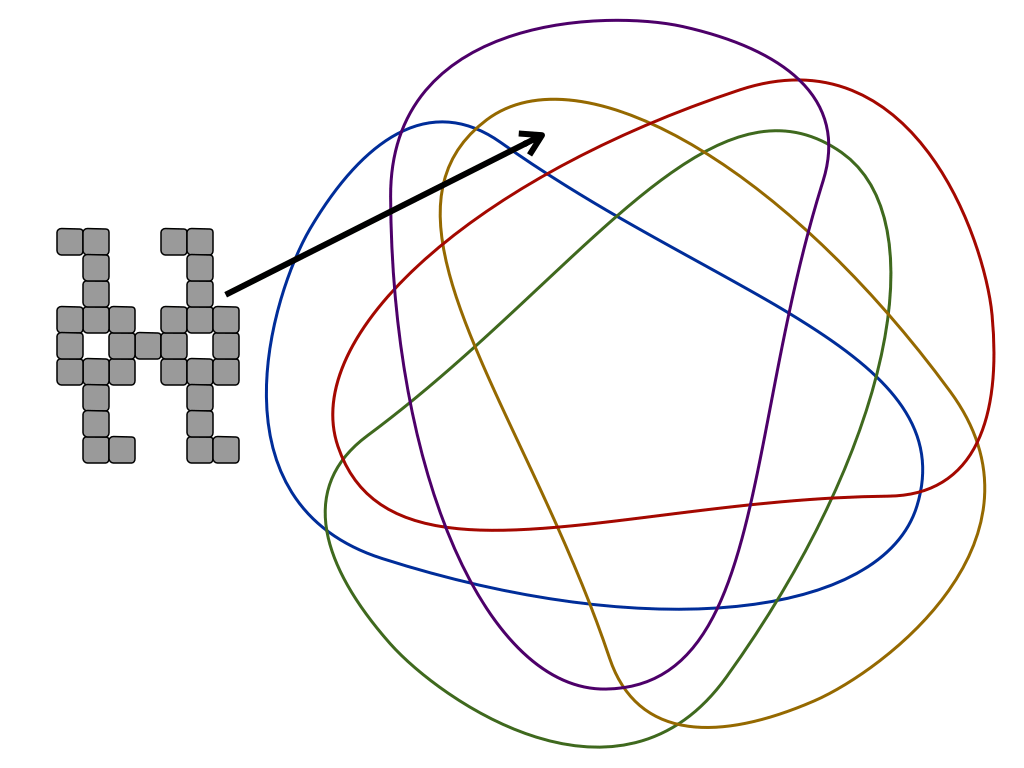Patterns

Give your grade 1 students a problem rich in pattern.

This icebreaker is great for any group to get to know one-another, but it is best suited to an elementary classroom learning about capital and small letters.

Introduce your elementary students to patterns, symmetry, order and chaos.

Kindergarten students argue about which beetles belong to the collectible family. The photographs of these beetles are from Dr. Udo Schmidt, a retired beetle collector in Germany. Thanks Udo!

A game to get your students talking about attributes. One player chooses a template and secretly chooses how to split the members of the group in two. Everyone else tries to guesses the rules governing the split.

Venn diagrams are not taught well anywhere.

With little effort, these diagrams can be brought to life with beauty and by going beyond that little 3 circle Venn diagram. At the very least a teacher should end a lesson on the three circle Venn diagram with a question: "I wonder if this is possible with four circles?"

But we can go much, much further... and the puzzle sheets created below are designed to get you there 😉

"Venn for Polygons" is a highly engaging puzzle that gives students ages 8+ practice with properties of polygons. All edges are the same length unless they are obviously different lengths. Thanks to student Calvin Chan for finding a shape that was a little wonky 😉

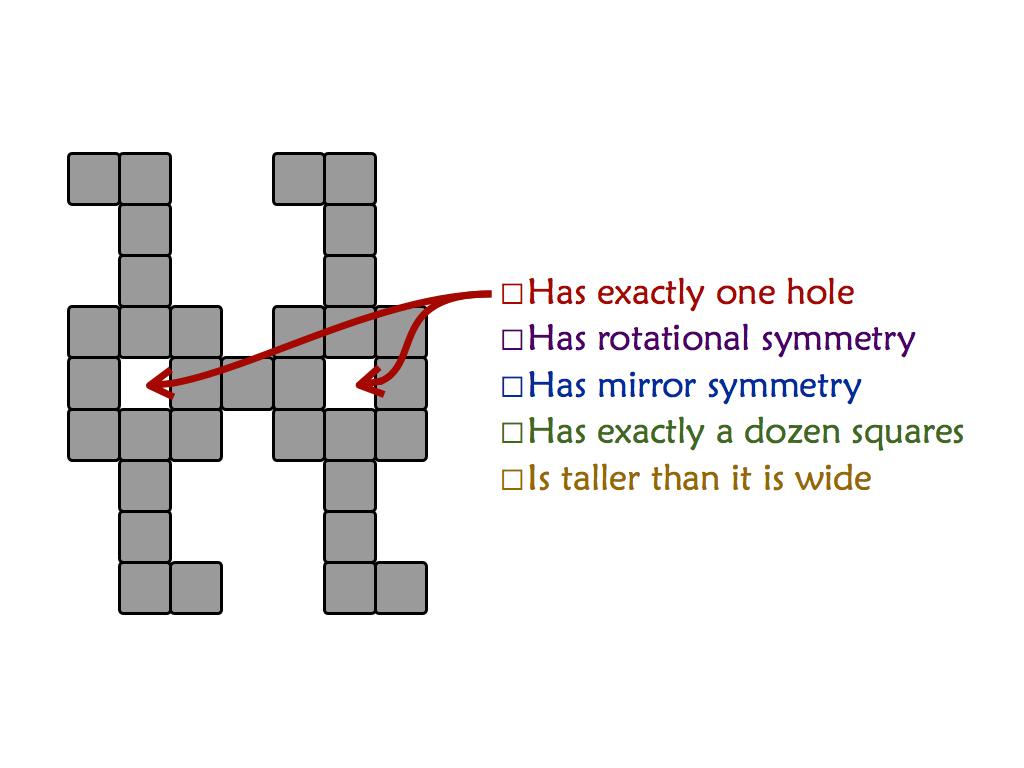
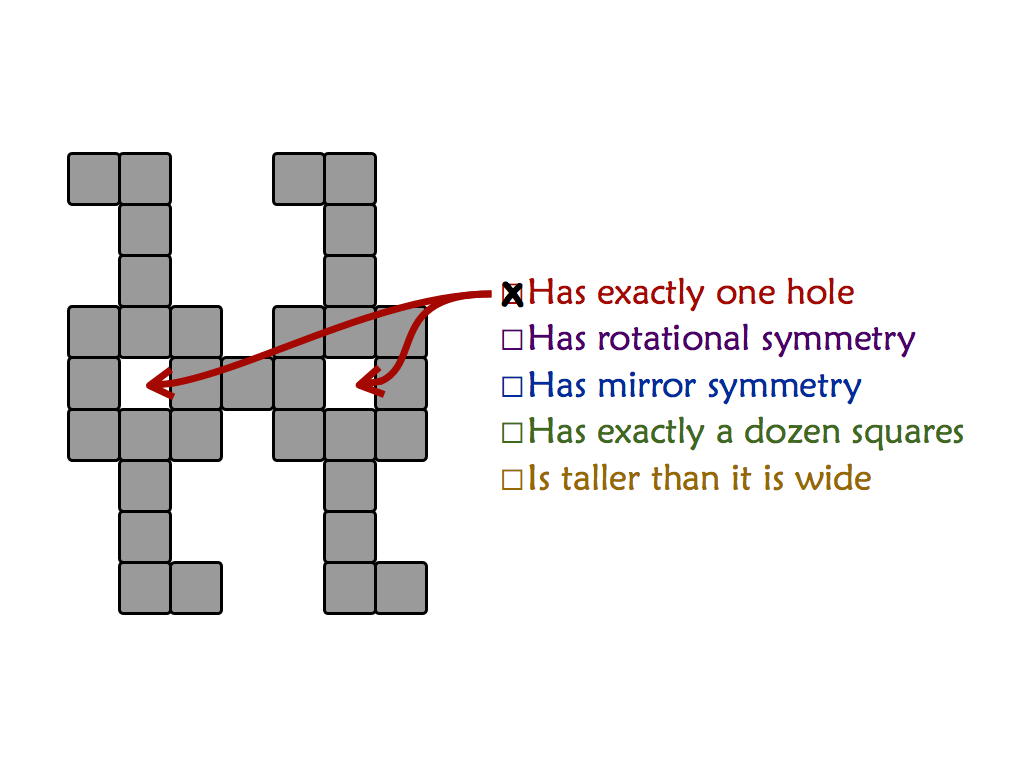
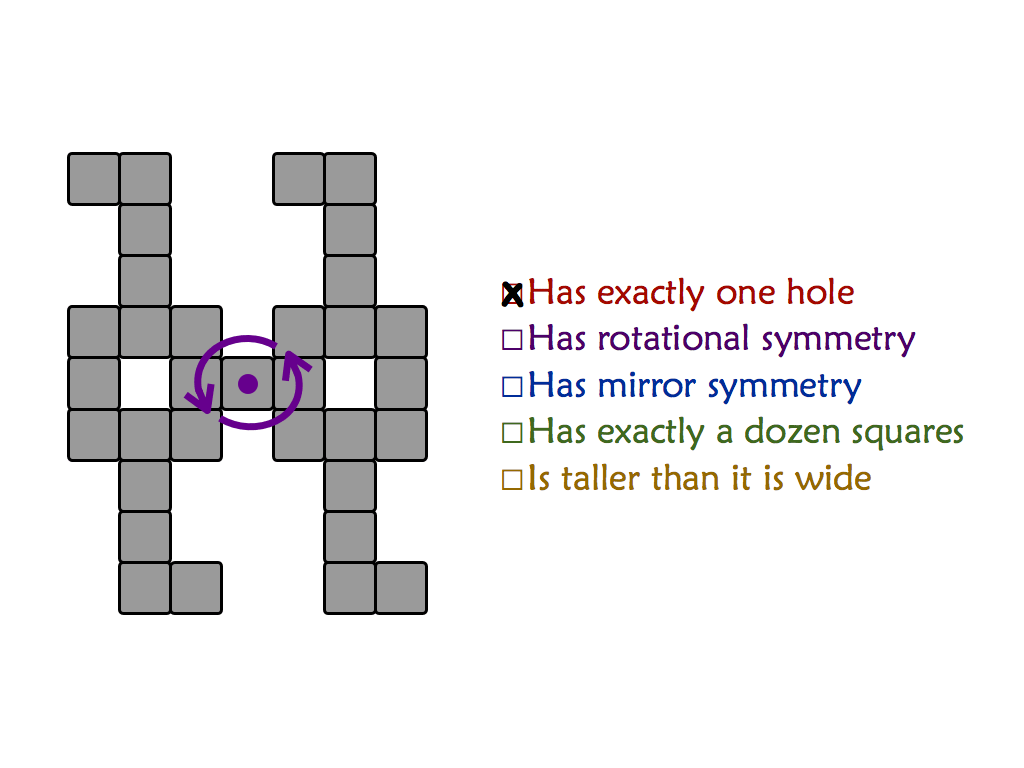
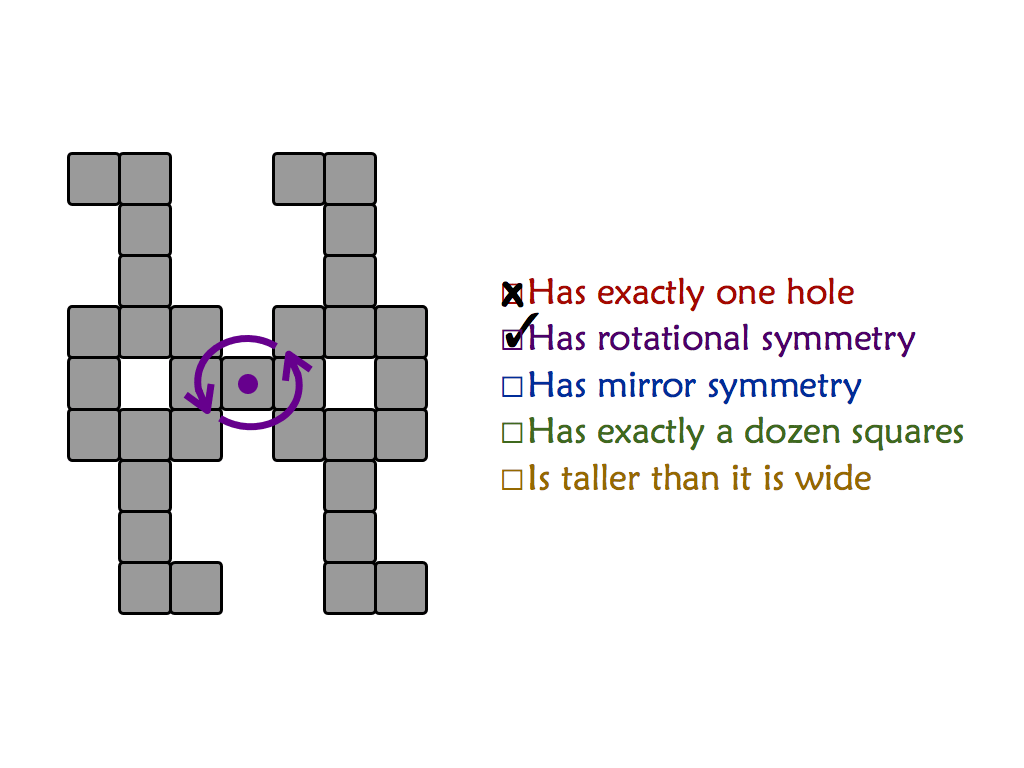
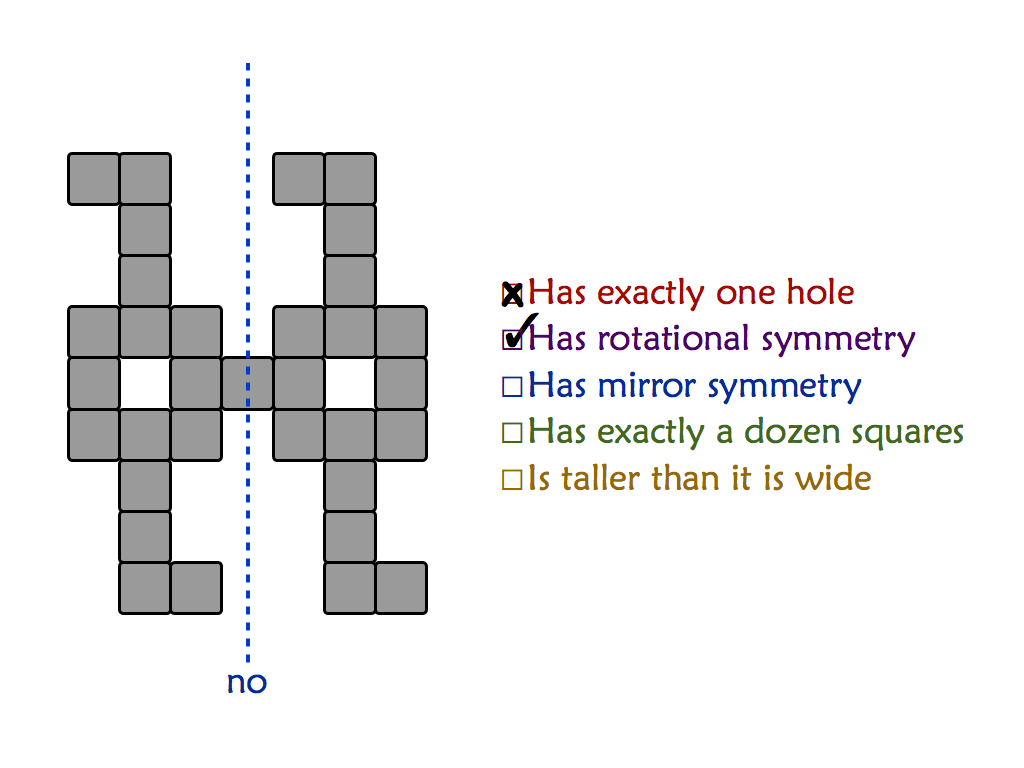
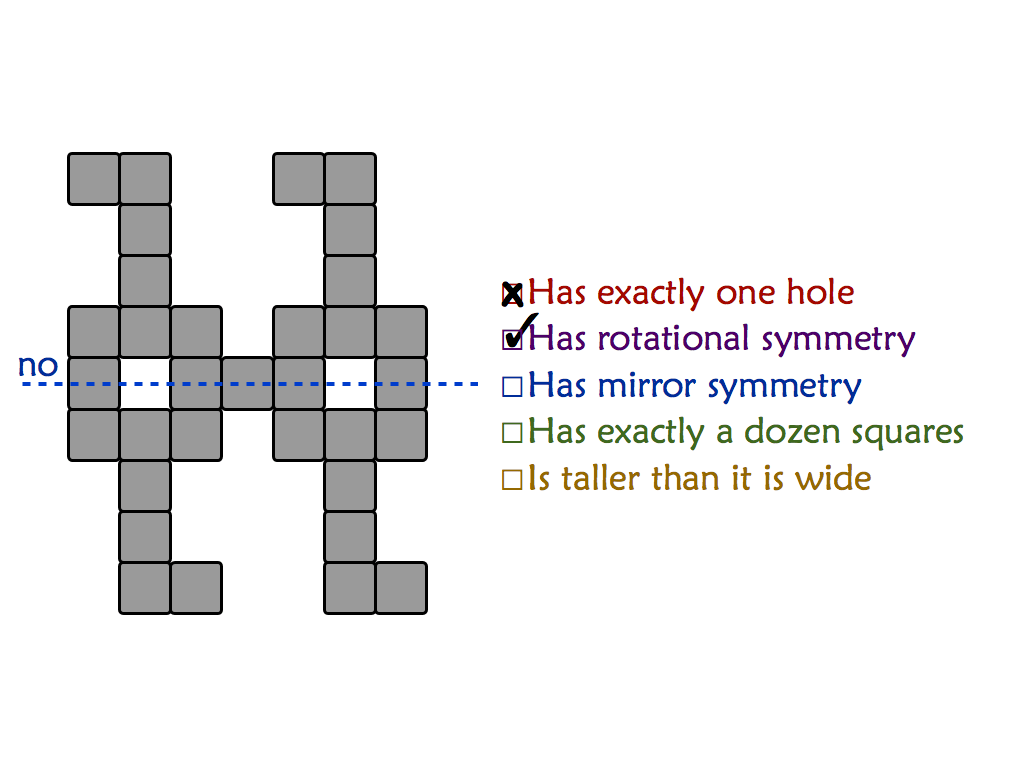
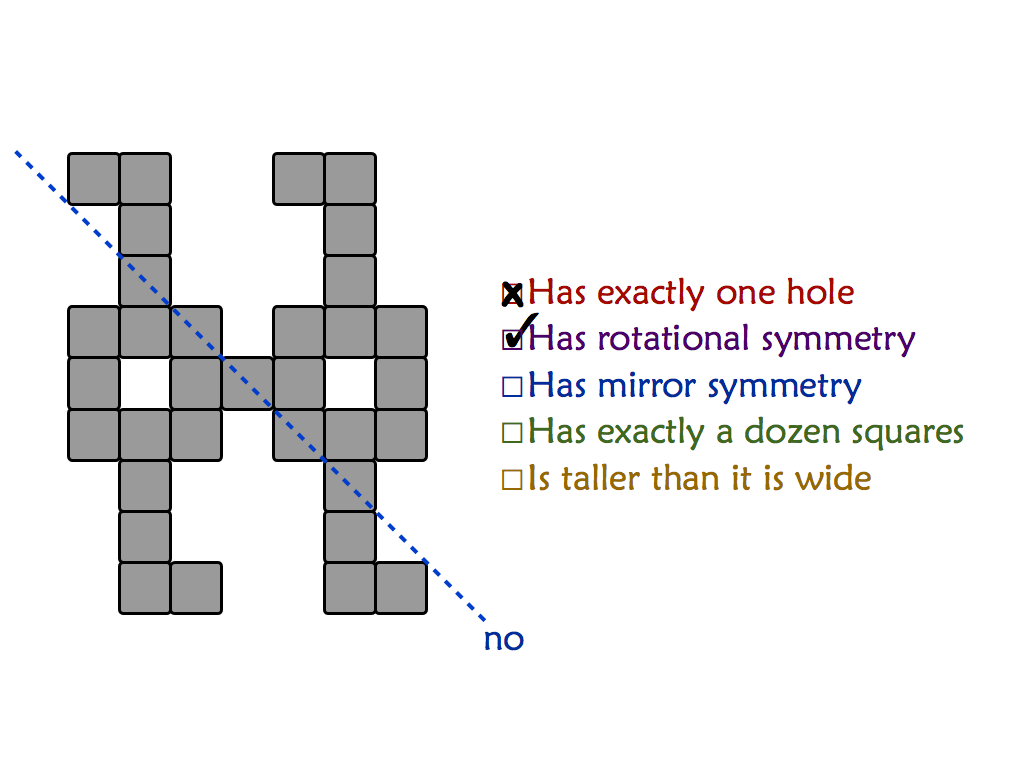
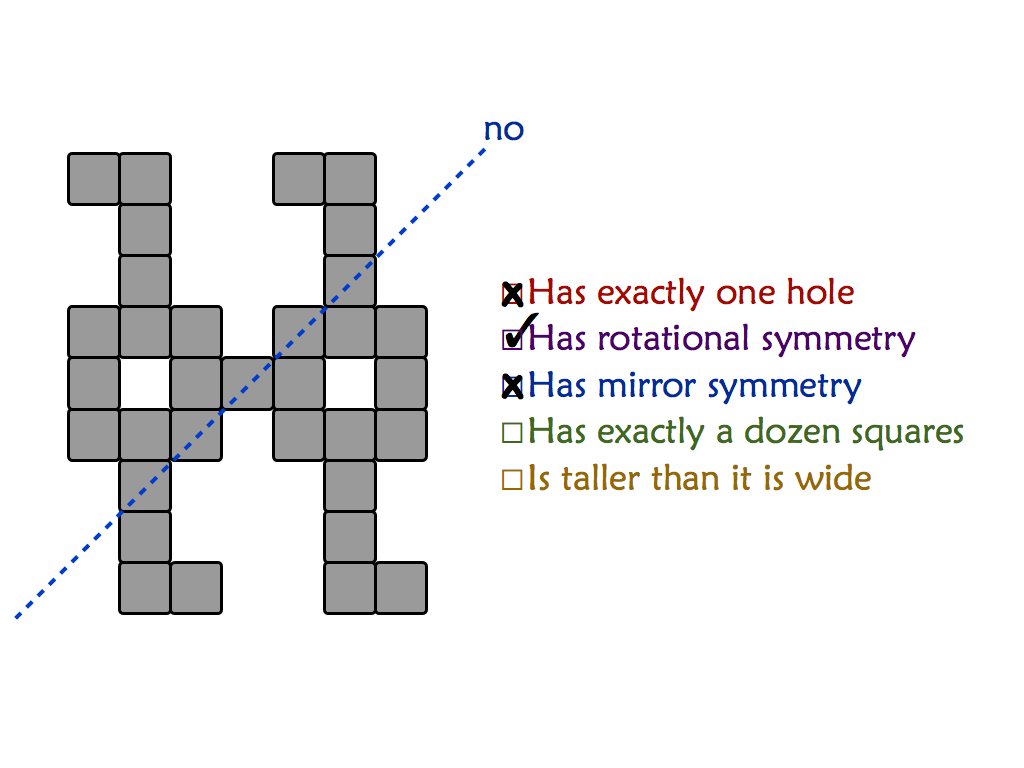
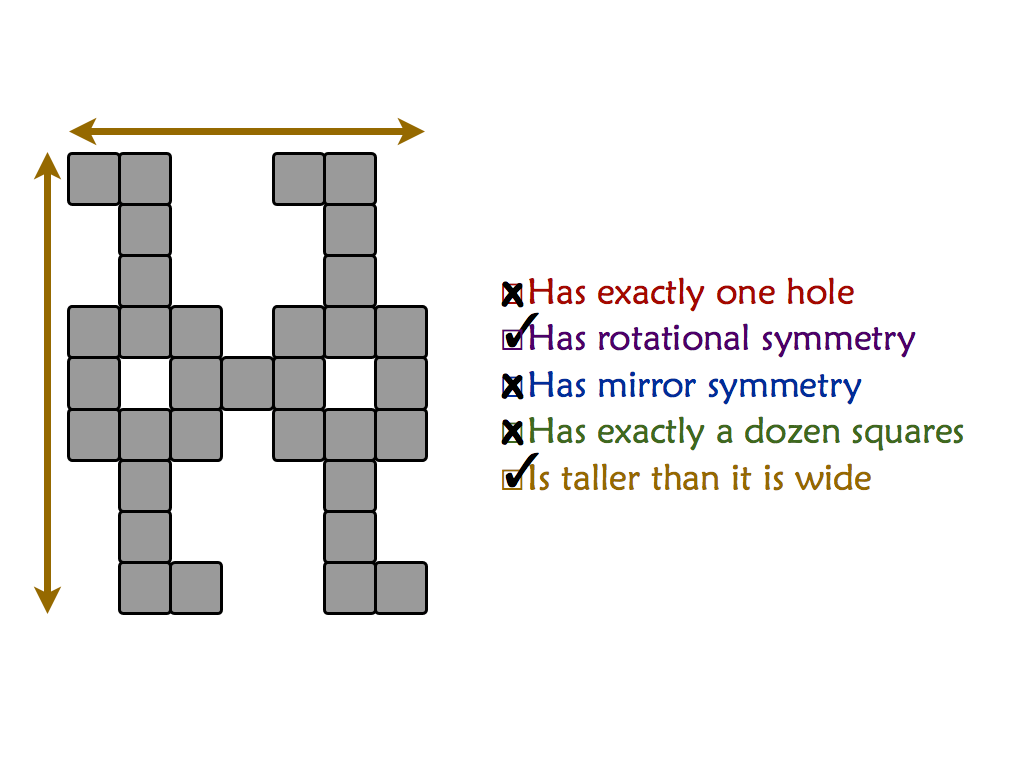
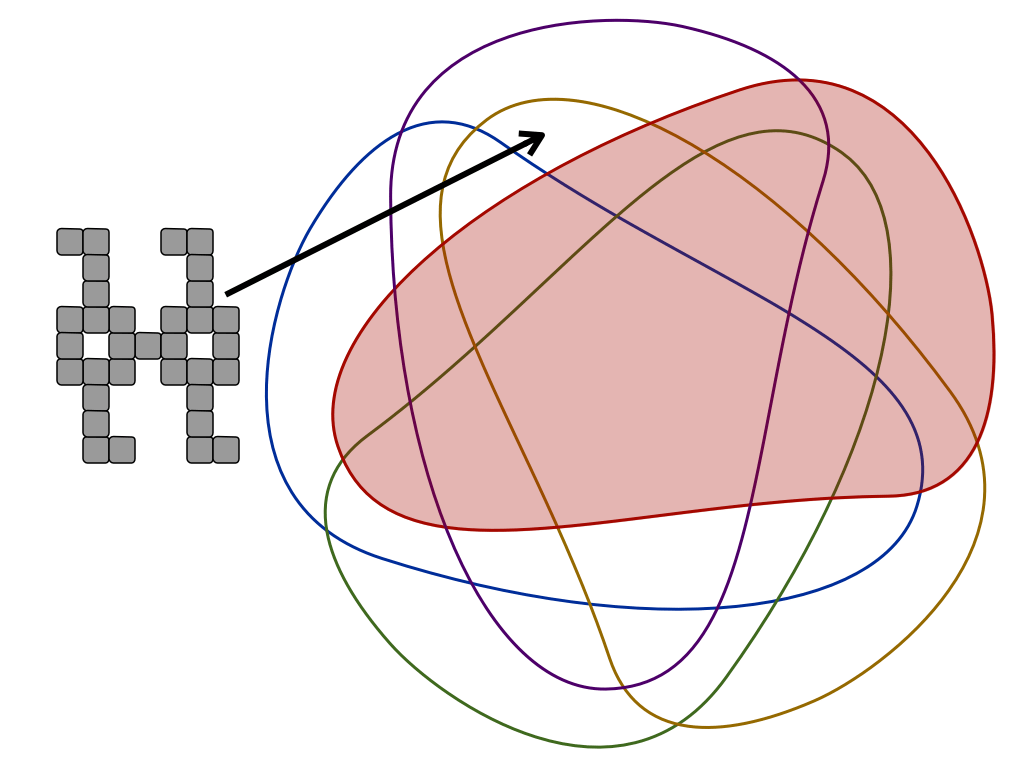
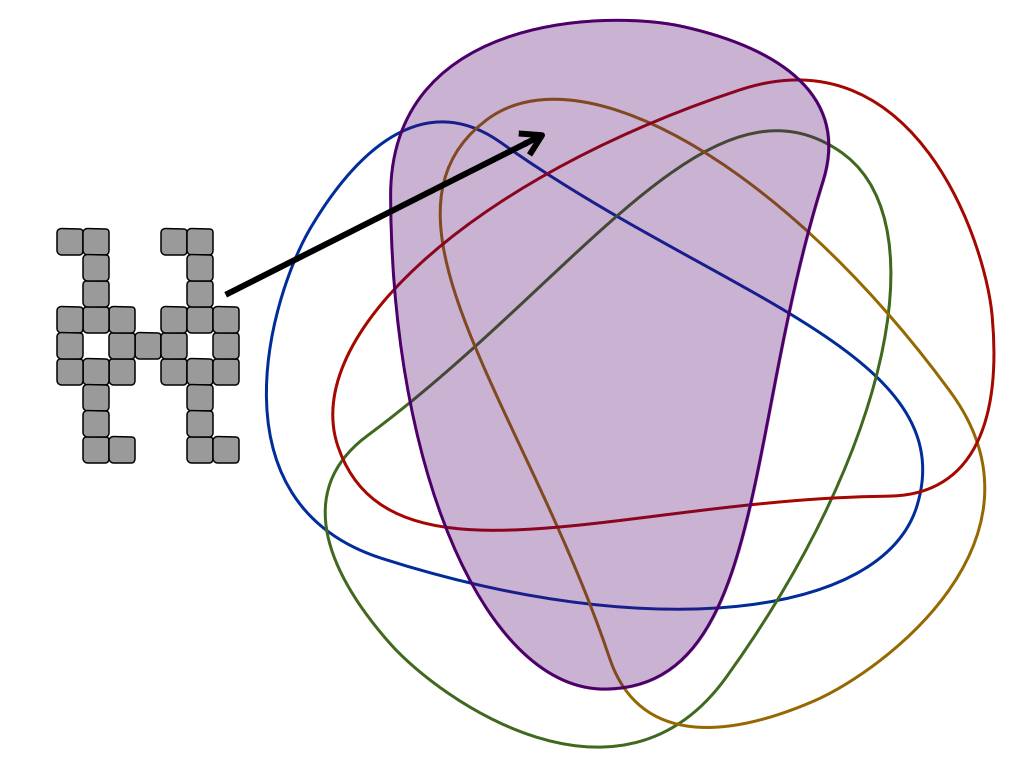
"Mishap at Venn Zoo" is a full presentation of a polyomino variant that includes rotational symmetry. This is good for students as young as 8 or 9.

"ToothPick Polygons" has got a tough second question, but the first part is as easy as "Mishap at Venn Zoo."

Mishap at Venn Zoo Find where all the animals go based on identifying the presence or absence of mirror and rotational symmetry, height, and size. Unfortunately the zookeeper might have made a mistake!

This is our zoo. There are 31 cages… 32 if you include the outside region. It is made up of five shapes in different colors. These colors will be linked to 5 questions we are going to ask about each animal.

These are the 32 animals that the zookeeper has mail-ordered to fill the cages. The expectation is that one animal will fit in each cage.

Let’s look at this Liopleurodon. Where does it go? The first question is about how many holes it has.

No – Liopleurodon does not have exactly one hole.

Does it have rotational symmetry?

Yes – it could be rotated 180 degrees around its centre and would look the same.

Has it got mirror symmetry. Not this way, but we need to check all the options…

Has it got mirror symmetry. Not this way, but we need to check all the options…

Has it got mirror symmetry. Not this way, but we need to check all the options…

No – Liopleurodon does not have mirror symmetry. Is its size exactly 12 squares?

No – it is much bigger than 12 squares. Is it taller than it is wide?

Yes – it is 9 squares high and only 7 squares wide. We have all the information to figure out which is Liopleurodon’s cage…

Yes – it is 9 squares high and only 7 squares wide. We have all the information to figure out which is Liopleurodon’s cage…

So does it go in the middle? No, this would be the cage for an animal that we answered “yes” to all the questions.

Does it go here? This does not look better. We answered “no” to the red question: “Has exactly one hole.” That means the cage for our creature must be outside the red loop.

Does it go here?

It is outside the red loop. Good.

It is inside the purple loop. Good.

It is outside the blue loop. Good.

It is outside the green loop. Good.

It is inside the tan loop. Good. Looks like we’ve found the right place. Now find out where all the animals go. You can download the puzzle-sheet above. It is the second one listed.

Kindergarten students experience mathematical pattern and structure in many of their books.

Use Unifix to play with patterns.

Math Puzzles do not get more beautiful than this one from Japan. It should be used by elementary instructors who need to give their students practice holding a ruler and drawing a straight line. They should also be used as an example of an inequality for students learning algebra.

Ruffian Ritual

Not everyone is nice. Not everyone even pretends to be nice, but their is still honour and protocol among thieves. Let's say that you're spying on a den of thieves and ruffians. The first thing you notice when they get together is that they all greet each other with a secret handshake (to be developed by your students.)

Thanks to David H. Lawrence XVII for this photo. I'm not sure if he's really a bad guy 😉

You need to pair them up so that each minute they are doing the secret handshake with a different member of the gang. They might start by doing the secret handshake with the person across from them.

They might then shake hands with one of their neighbours...

... and then the other neighbour...

They are finished their ritual and can now get down to their dastardly business. But what happens if a different number of these ruffians gather together?

The ruffians will very quickly figure out that they are doomed to failure if they are an odd number. Odd numbers don't work because the thug that is left out of the first handshake ritual will likely feel thwarted and get violent.

You can see the disaster here...

... and you can see the ruffian who justifiably feels left out.

What about six thugs? Can they meet and get all their ritual hand shaking done so that every minute every thug is shaking the hand of every other thug? Again they could start out with those standing opposite...

Then they could shake their neighbours...

... and the other neighbour...

Each thug has two thugs left to shake hands with...

... does this look good?

No - two of these thugs have already greeted each other. Your fist task as a class is to figure out how six thugs can shake each others hands. Your second task is to figure out how many thugs can come to one of these subversive meetings. Is 8 possible? Is 10 possible? Is there an upper bound that limits the maximum gathering of these nefarious characters?

Spoiler alert - the next slides highlight a solution found by one of my grade 8 students (Matt Slavin) to the 8 ruffian puzzle. Do not show this to your class! Do not even look at it yourself until after your class and you have struggled for a period. Somebody will probably find a different solution and that is far far superior to you entering the class like a god or goddess smugly knowing the answer. It is much more exciting for the students to see their teacher struggling along side them. I did not solve this problem myself. There is no embarrassment in trying and failing. What a fantastic role model you will be to your class. Please stop here.

Matt's idea was to break up the group of eight ruffians into two groups of four. In three minutes each group can handshake with each other. We've already seen how to solve the four ruffian problem. Now what do the ruffians do? The two groups don't know each other. They decide to line up.

Now they do their secret handshake greeting with the person across from them. PS. Notice the hairy guy in the top left. He's part of the red group. He grew hair just so we can track what he does 😉