Primes & Composites

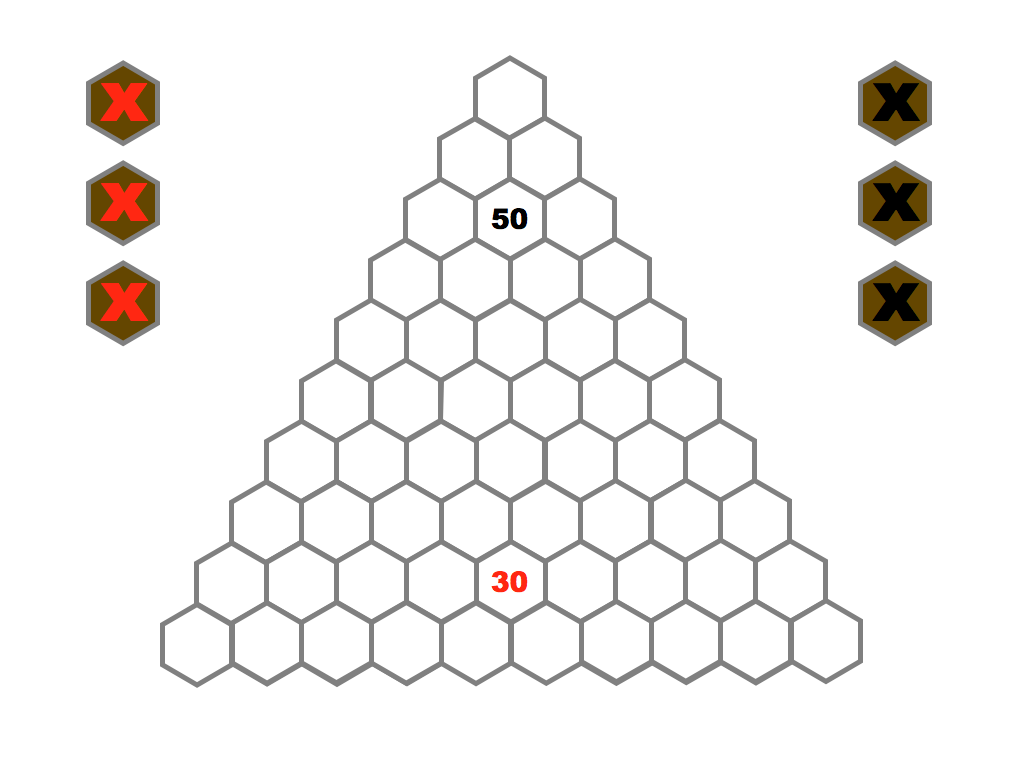
Integral fission is a variant of prime factorization trees allows the creation of a treasure trove of puzzles. The newest puzzle is to find the first time each Integral Fission shape is encountered. Download the Puzzle-sheet, instructions and solutions here.

GCF Bingo is a game where students can both strategize and gain practice calculating the greatest common factor of a set of numbers.

Download the pdf for the game here.

This is one of the must-play games in your classroom whenever you start tackling prime and composite numbers. References to the $1,000,000 prize are a long way away, but I hope one day to be able to tell you all that it is true.

Attached is a pdf game-sheet for your students.

Klingon Attack

The Earth is being attacked by Klingons. It is your job to shoot the enemy spaceships out of the sky using our single ion cannon. Download a pdf of puzzle-sheets here.

Much thanks to Ex Astris Scientia for their permission to reprint their engaging starships.

To save Earth we must fire our ion cannon - starting at the rear of the ship. Ask the students how long they want to wait before they target the upper left deflector. They might say "10 seconds." You re-phase it "time 10" so students understand that this puzzle can be played slowly.

A new student is asked to supply the time for the disk below. At this point, the students do not know the rules. Our first objective in to engage. If you start by trying to teach rules you will lose 10%-15% of the class. You engage students by asking them to contribute...

The next student says "time 15."

The next student says "time 8."

No hands are raised. You methodically go through all students.

The next student says "time 12."

The numbers in the next row must be either the sum of the two numbers behind - or a factor of the two numbers behind. So ask the next student what they want for the number in front of the 10 and 15.

10 + 15 = 25... so 25 is a possible answer.

5 is a common factor of both 10 and 15, so 5 is another possible answer. (1 would be another possible answer.)

Let's say the student says "time 5."

The next time in that row could be 1 or 23.

Let's say the next student said "time 1."

...and for the last one a student might say either 8 + 12 = 20 or 4 (4 is a factor of 8 and 12), or 2 or 1.

It may need to be emphasized that low numbers are better (I have not told you why yet.) A wise crack student who insists on a huge number (like 1,000,000) needs to be dismissed without giving them attention - and the next student chosen.

The student chooses "time 20."

Just let's skip forward quickly to the end...

So we have finished! How long did it take us? What is the largest time?

Let's say back at this shot we chose differently. We chose the 4. Let's step forward to the end...

So this might look better. It looks like we have 15 as the highest number which might mean that we would save Asia. Unfortunately that would be wrong. What's wrong here?

At time 5 we are confused. "There are two places we have to shoot! The enemy ship penetrates Earth's defences - the Earth is destroyed! Drats."

Duplicate numbers are not allowed.

Negative numbers are not allowed, but zero is allowed (however students might discover something interesting if they use zero.)

Download a pdf of puzzle-sheets here.

Choose a number. Find all of its proper divisors. Add them up to find a new number. Repeat. What happens? That’s what we are going to explore in this quirky visit with Tweedledum and Tweedledee.

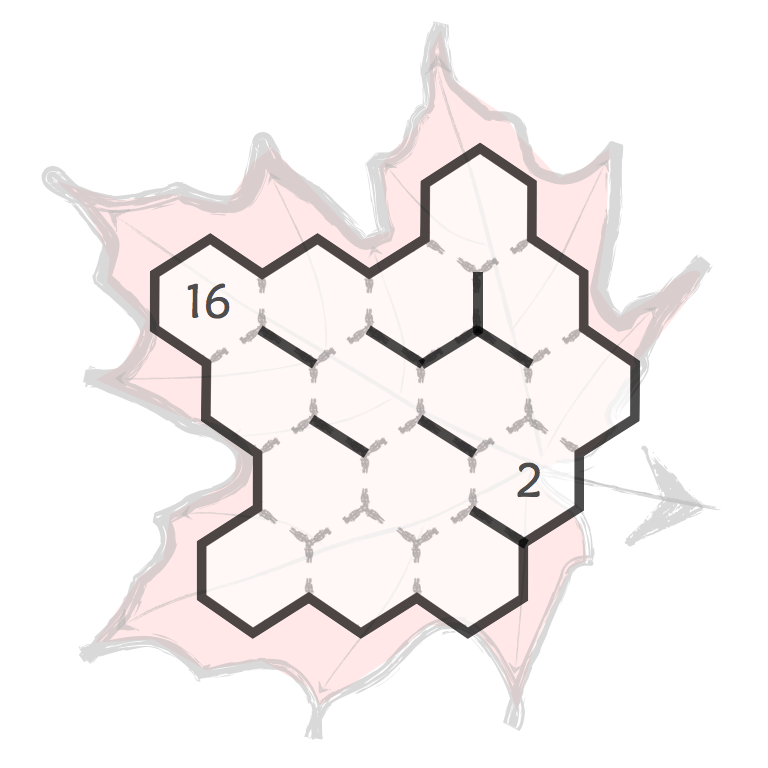
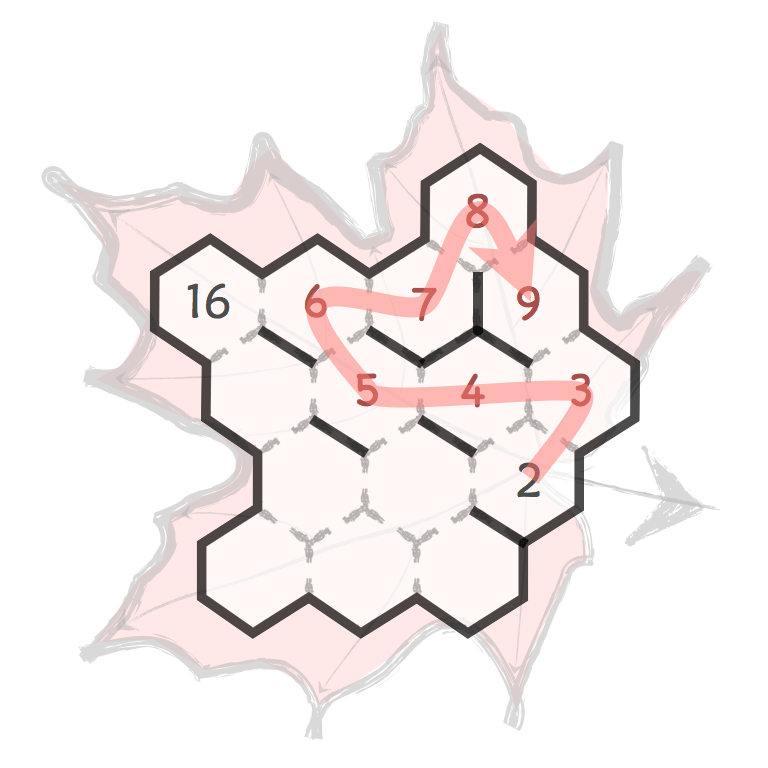
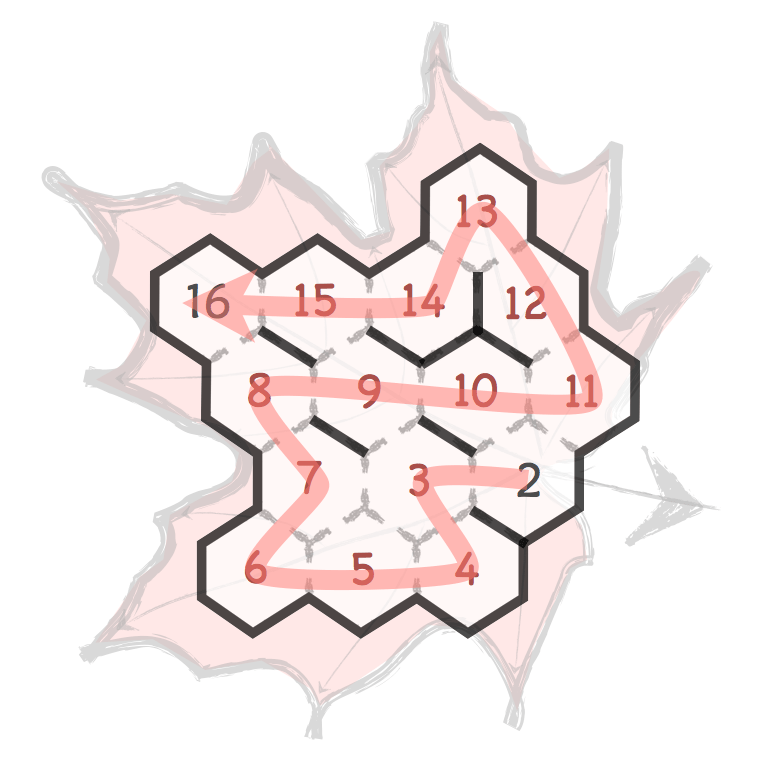
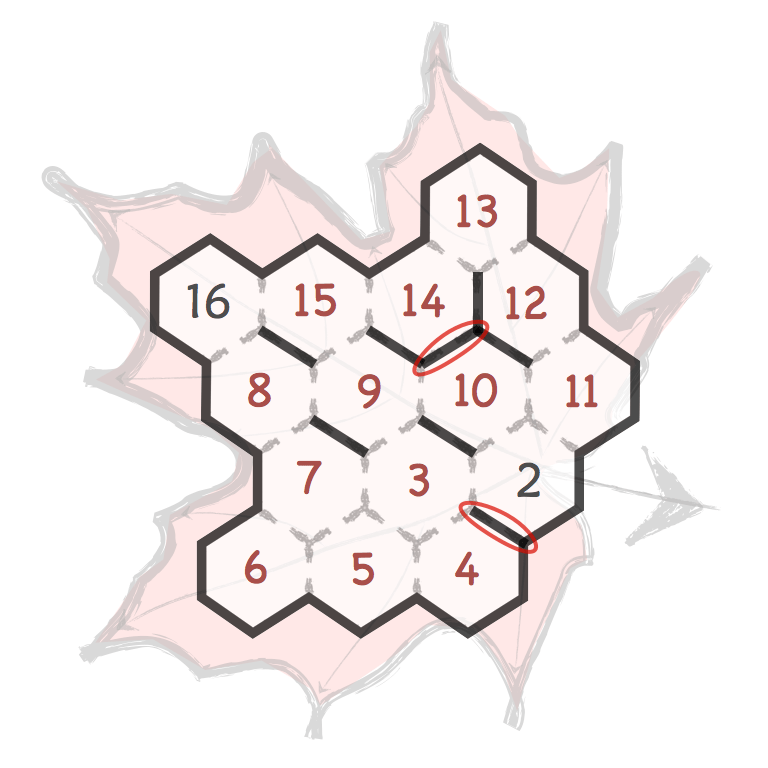
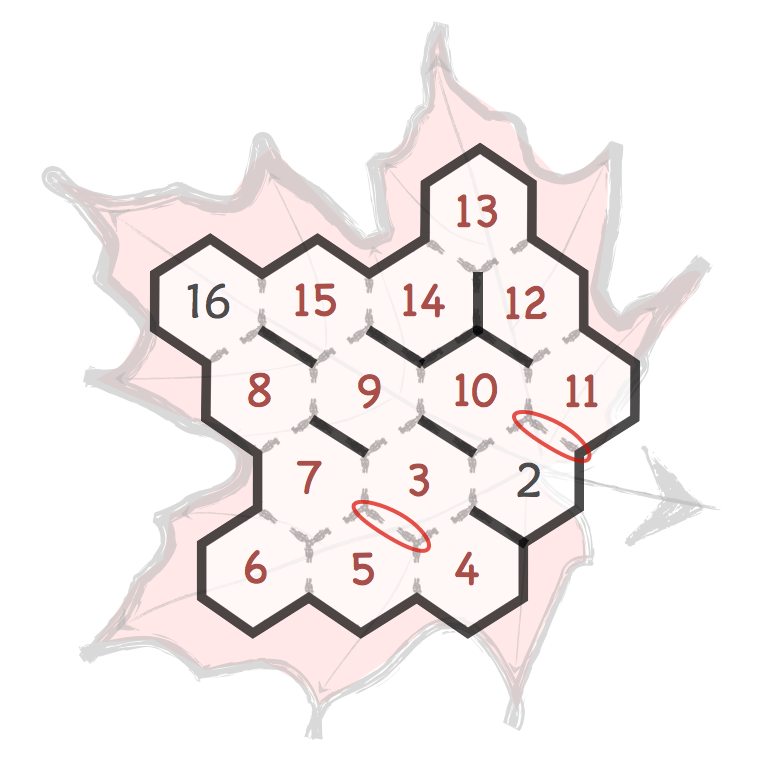
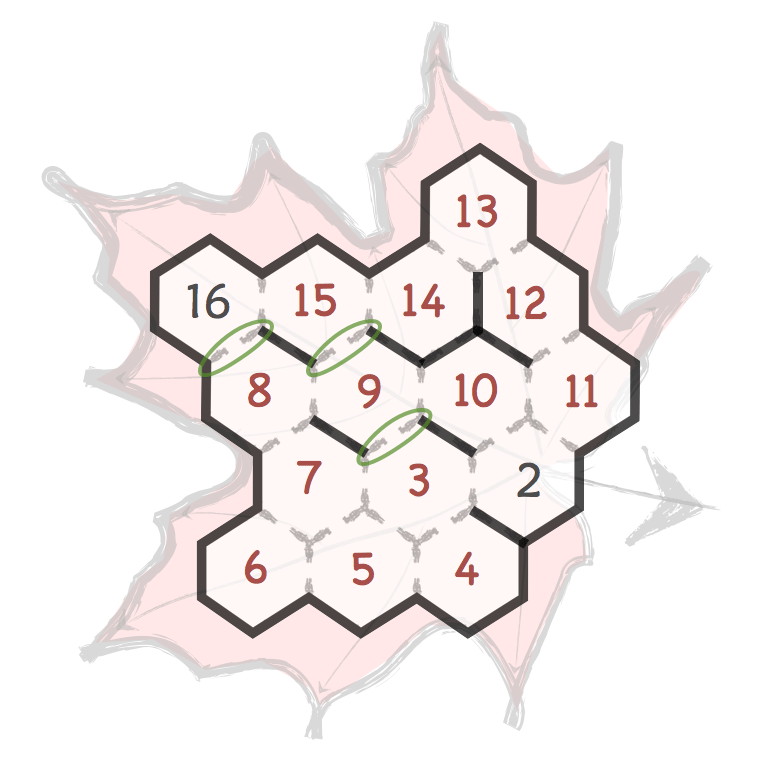
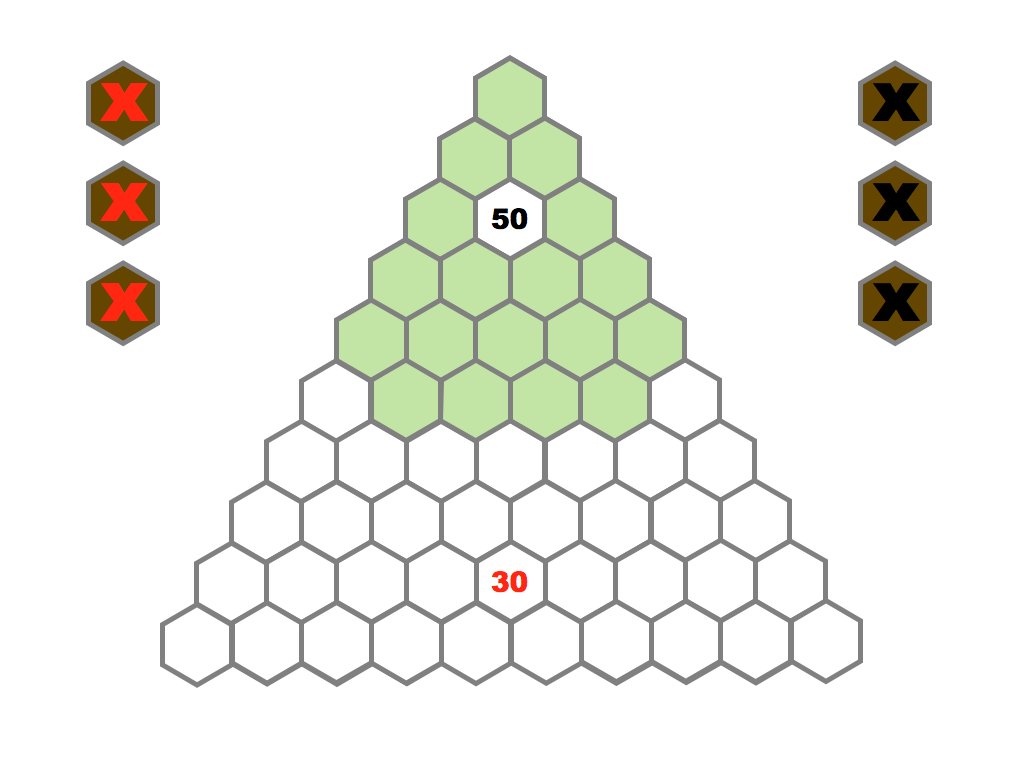
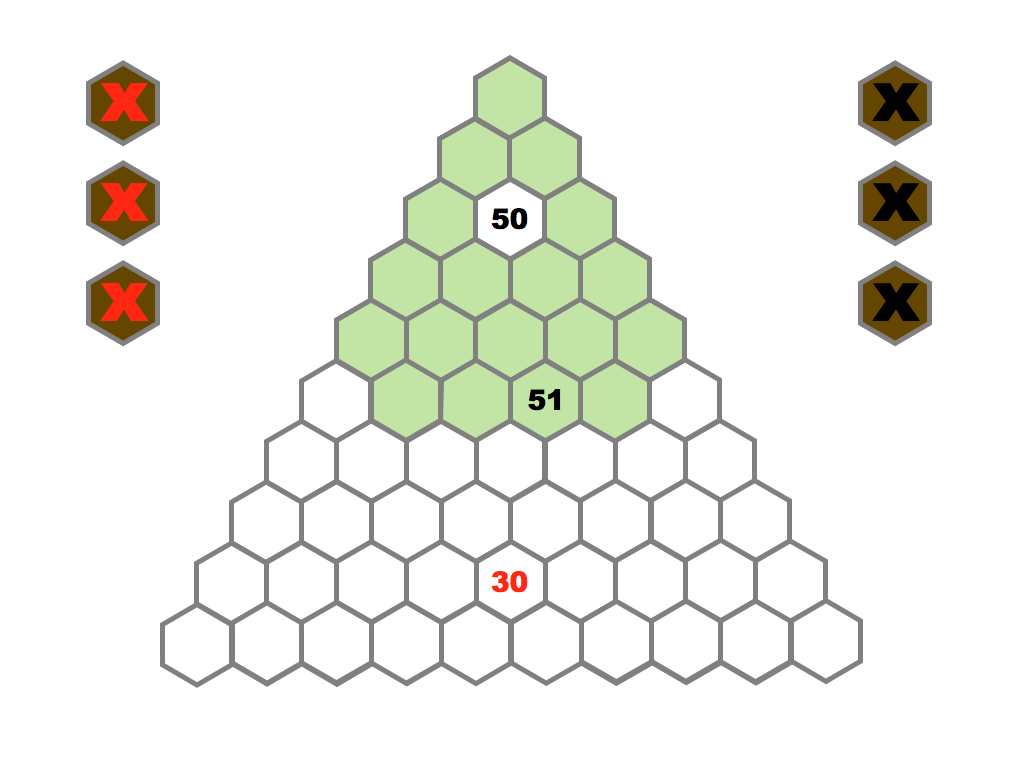
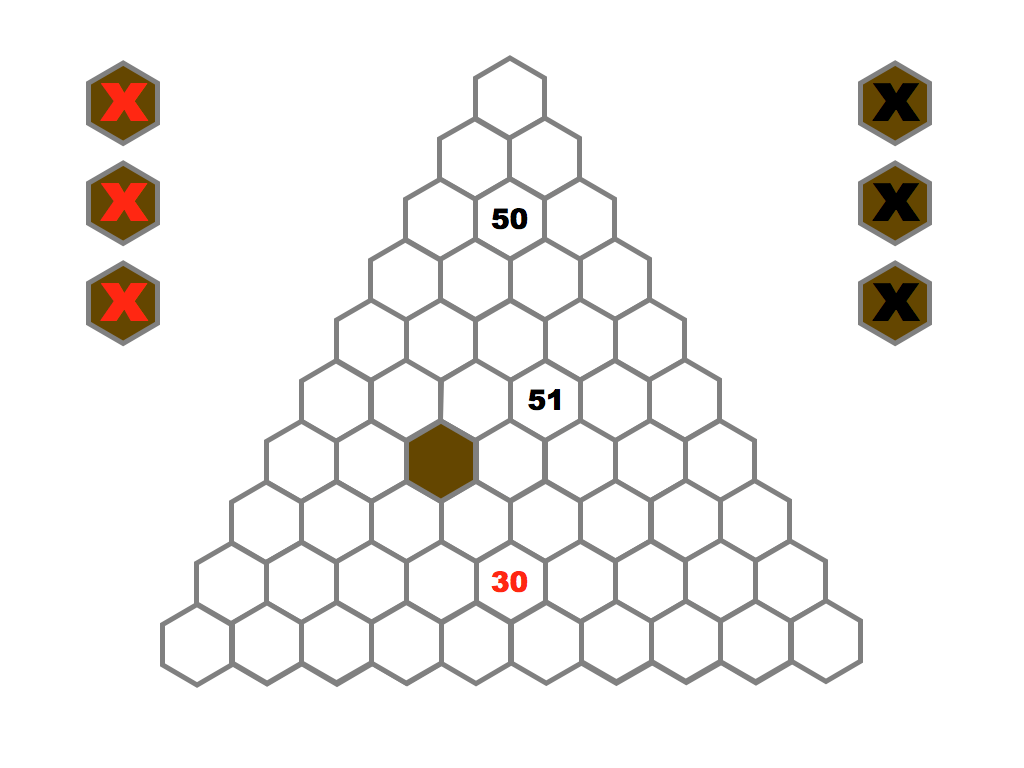
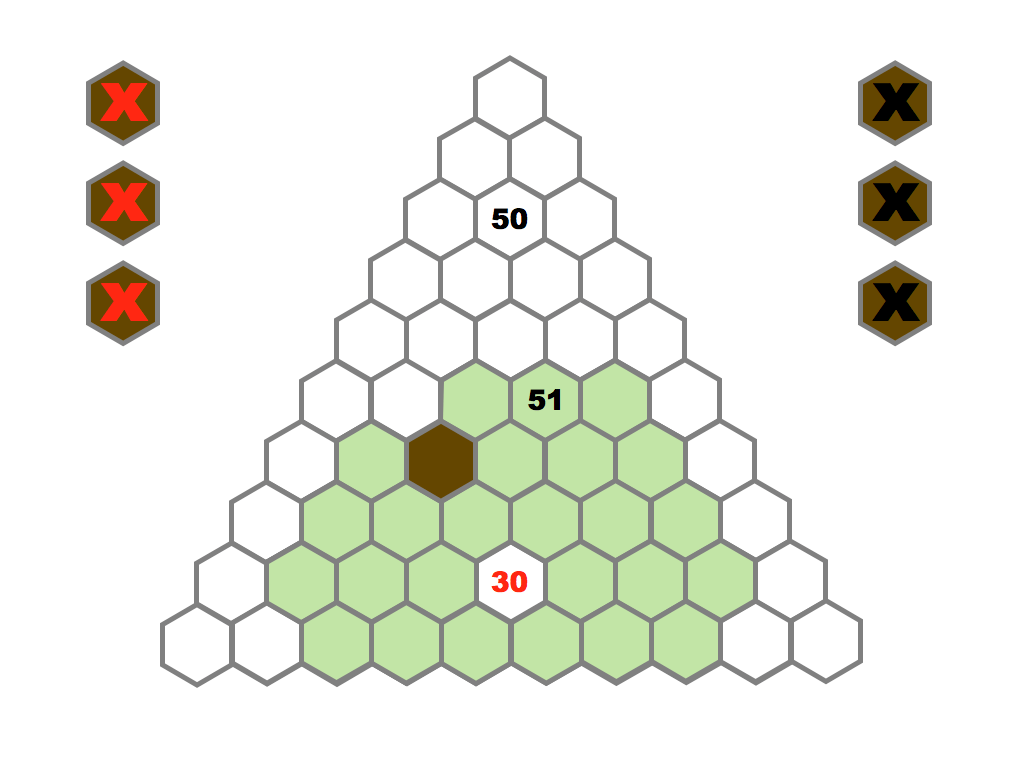
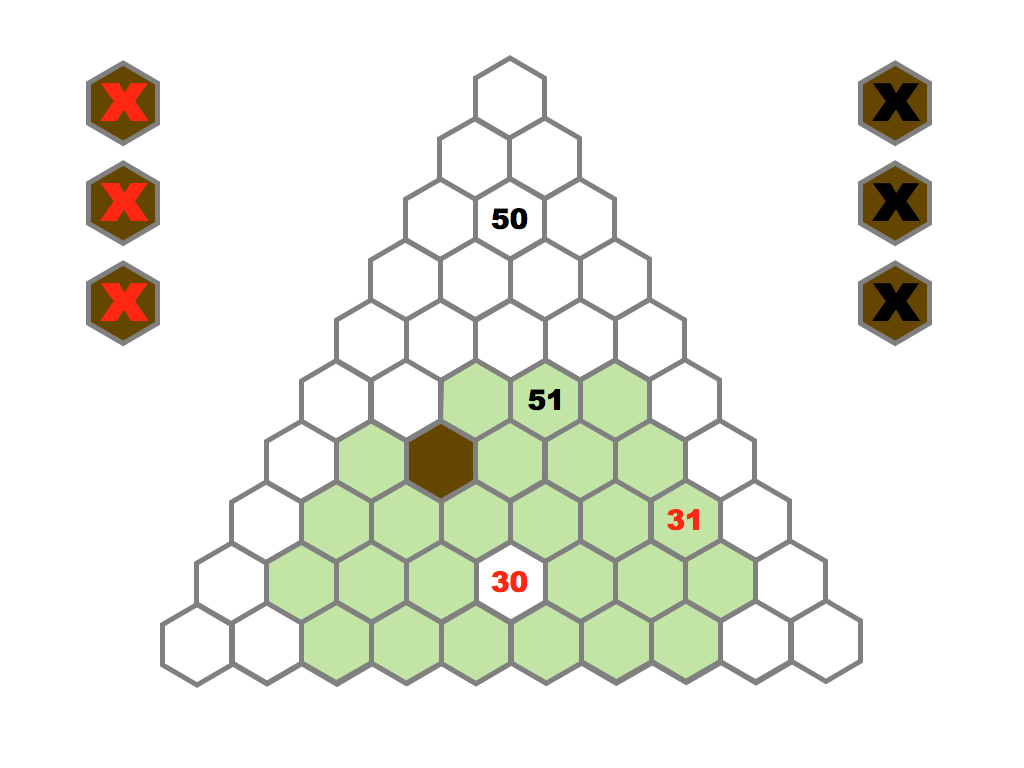
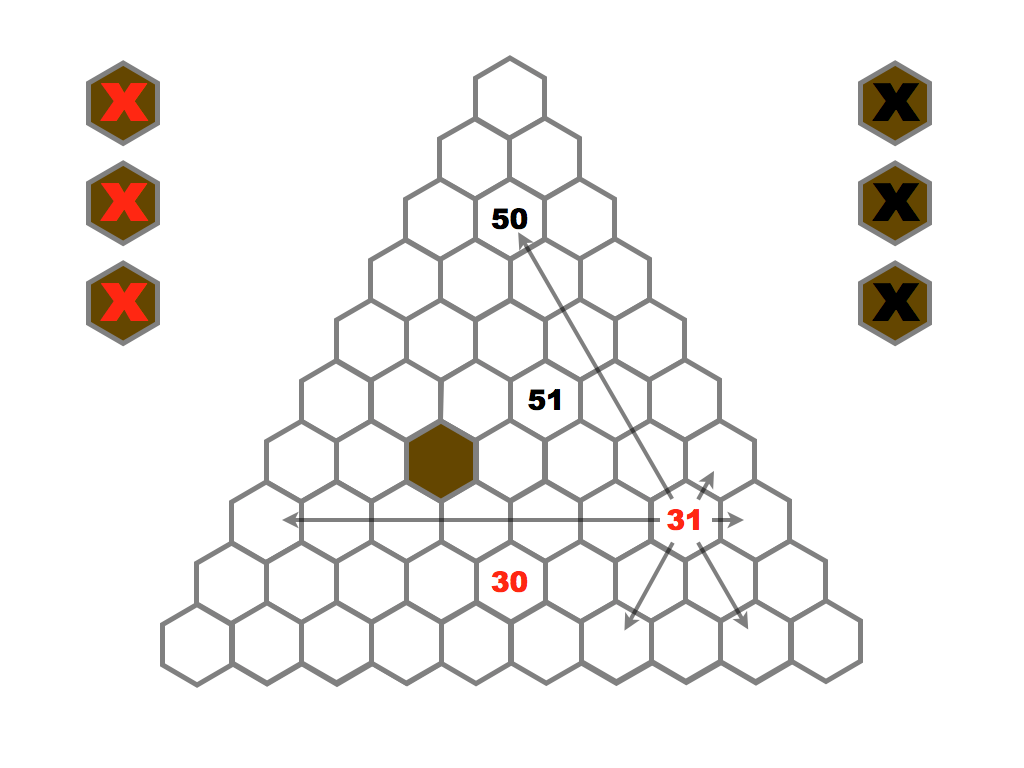
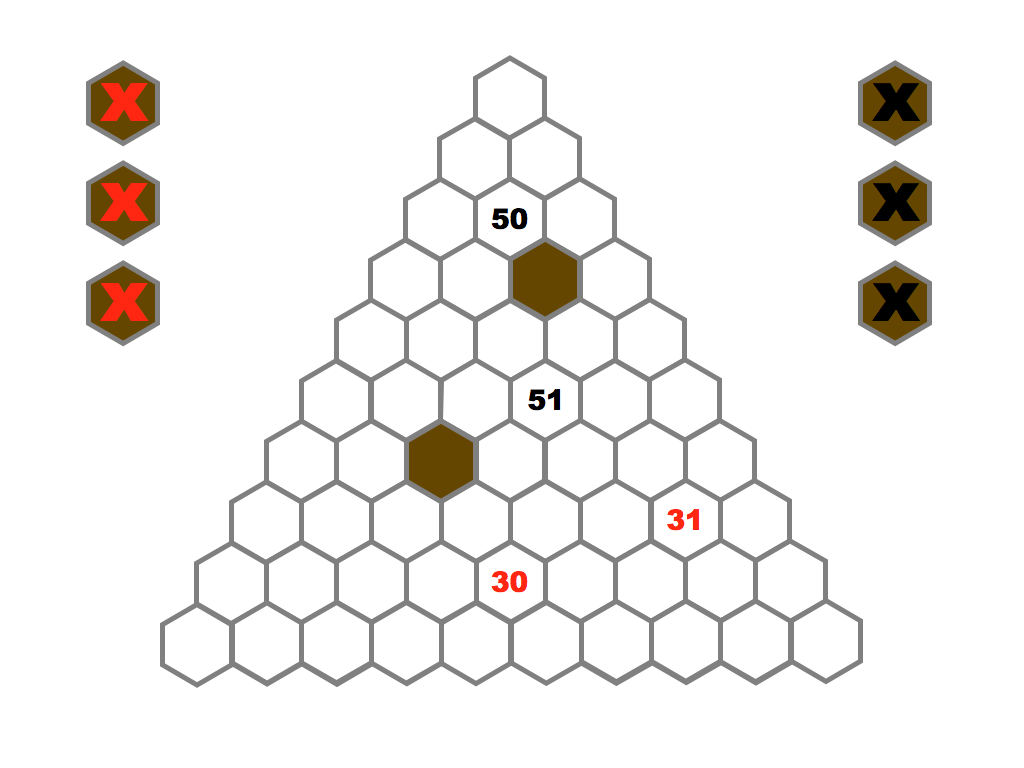
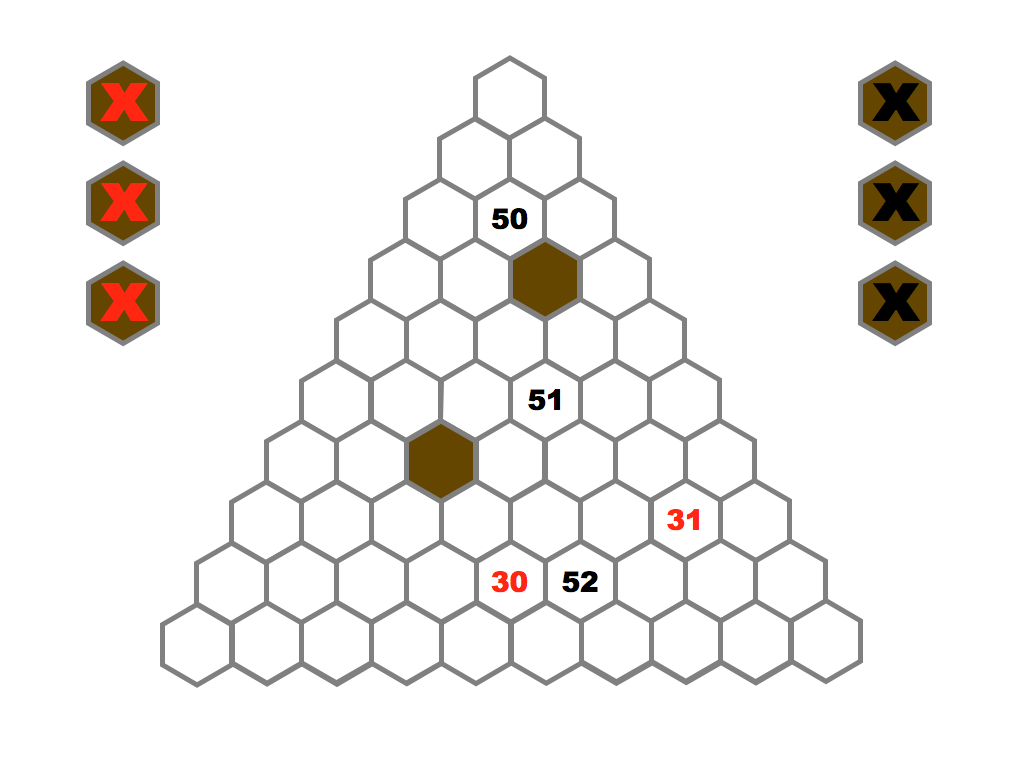
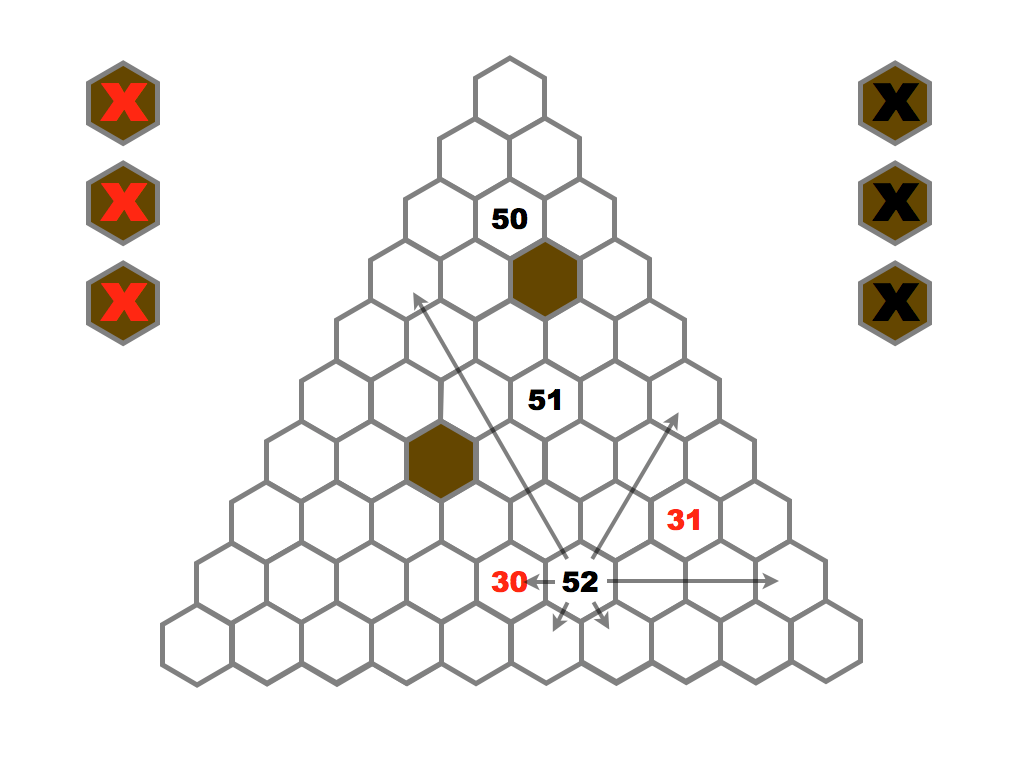
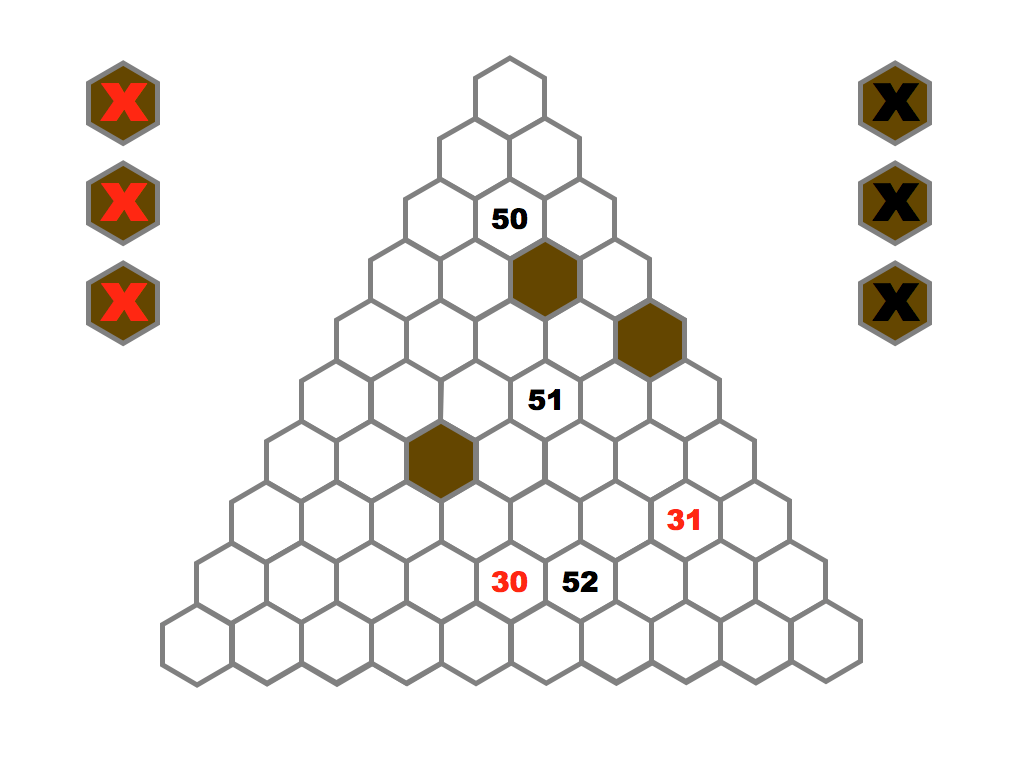
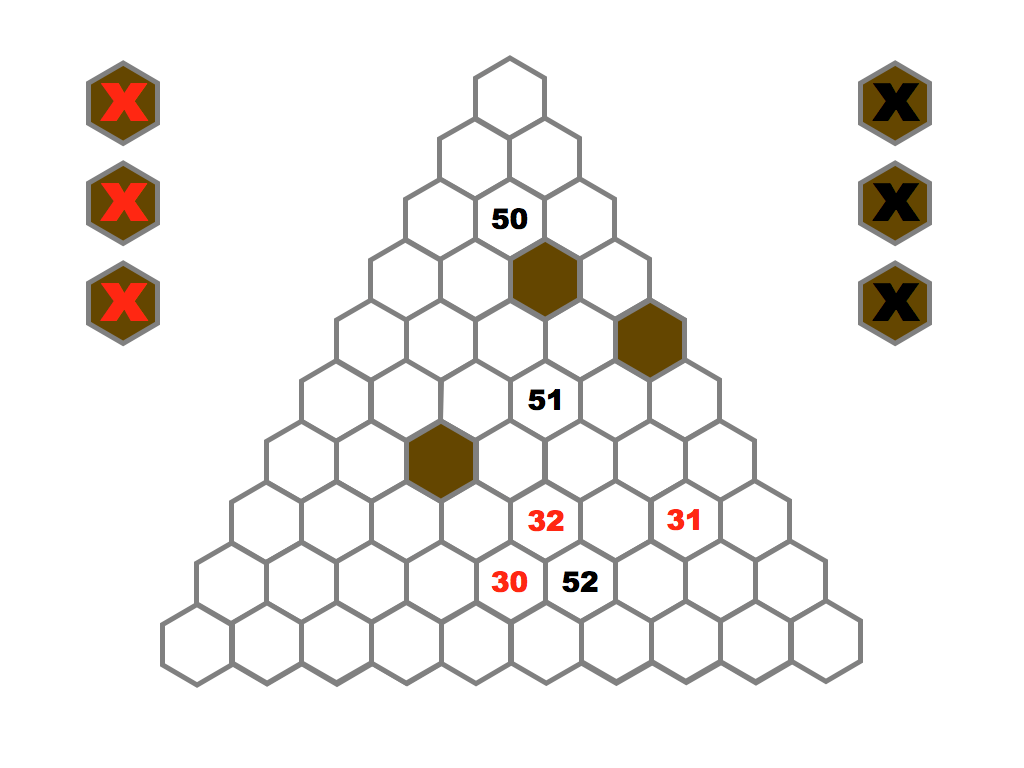
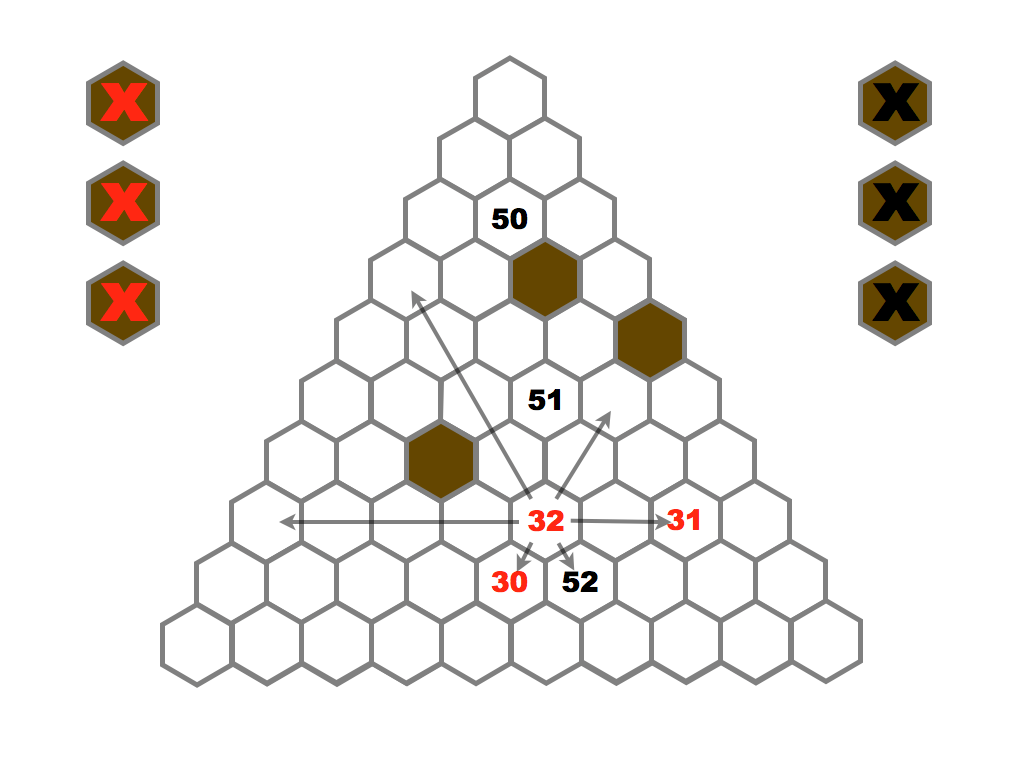
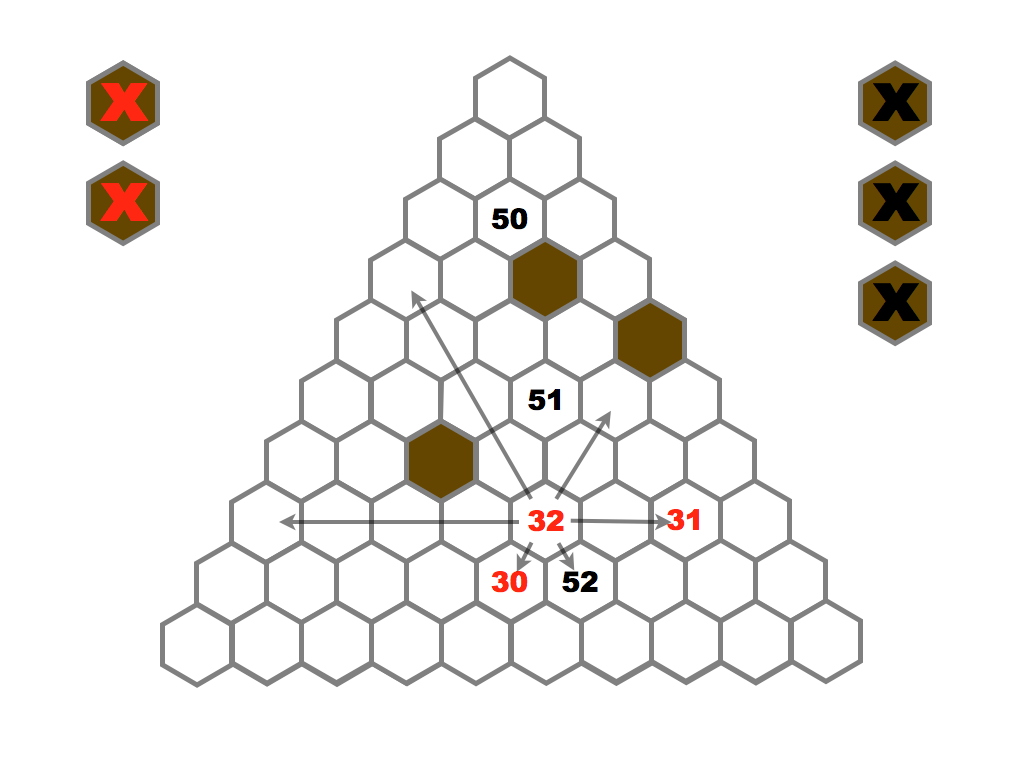
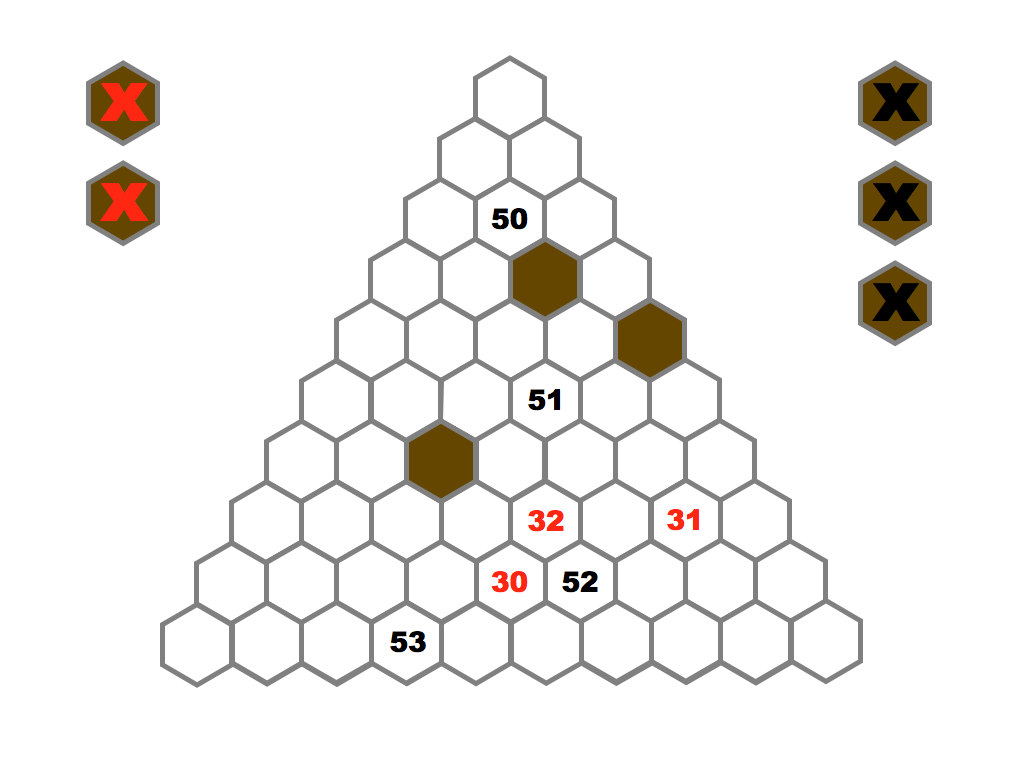
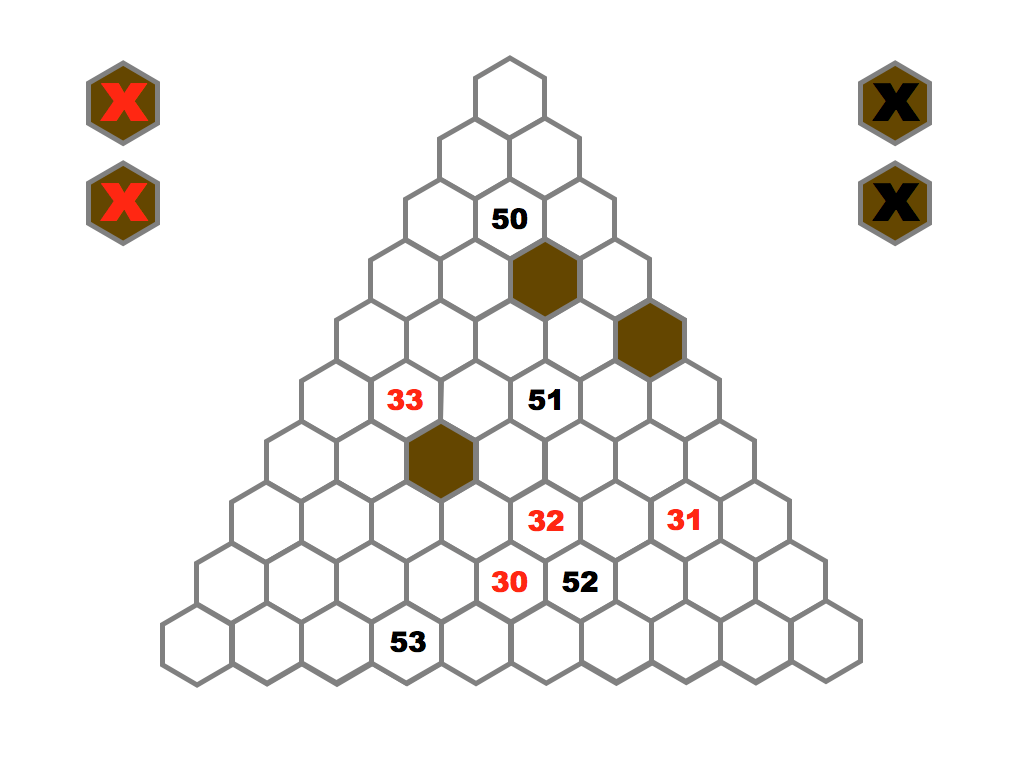
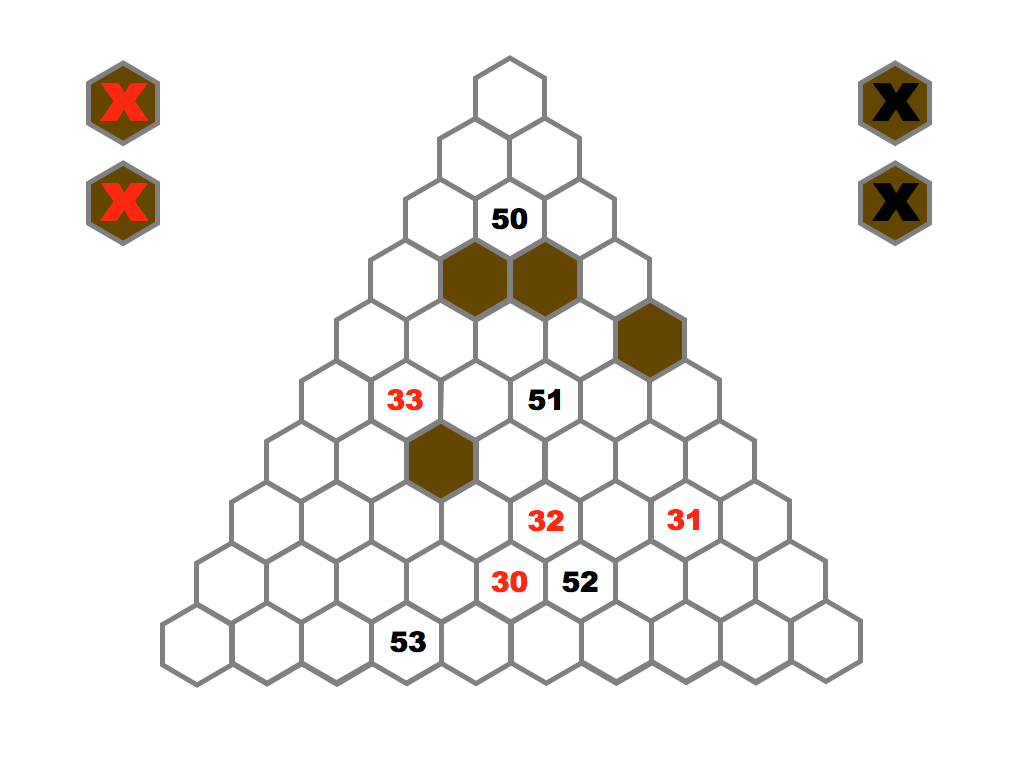
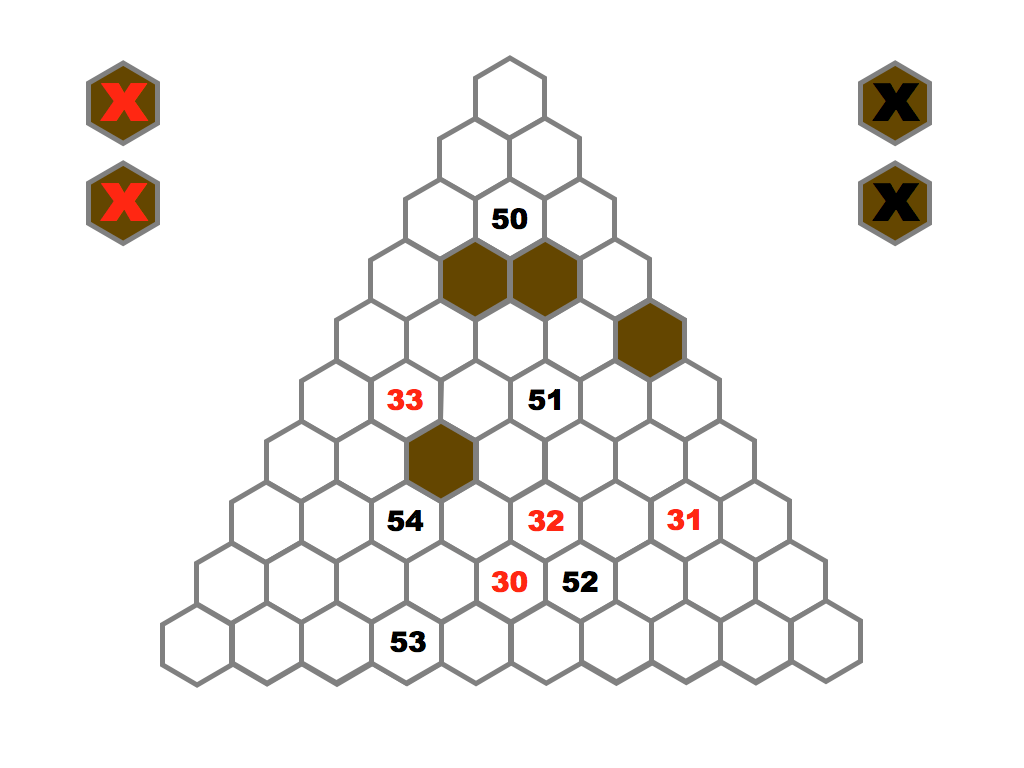
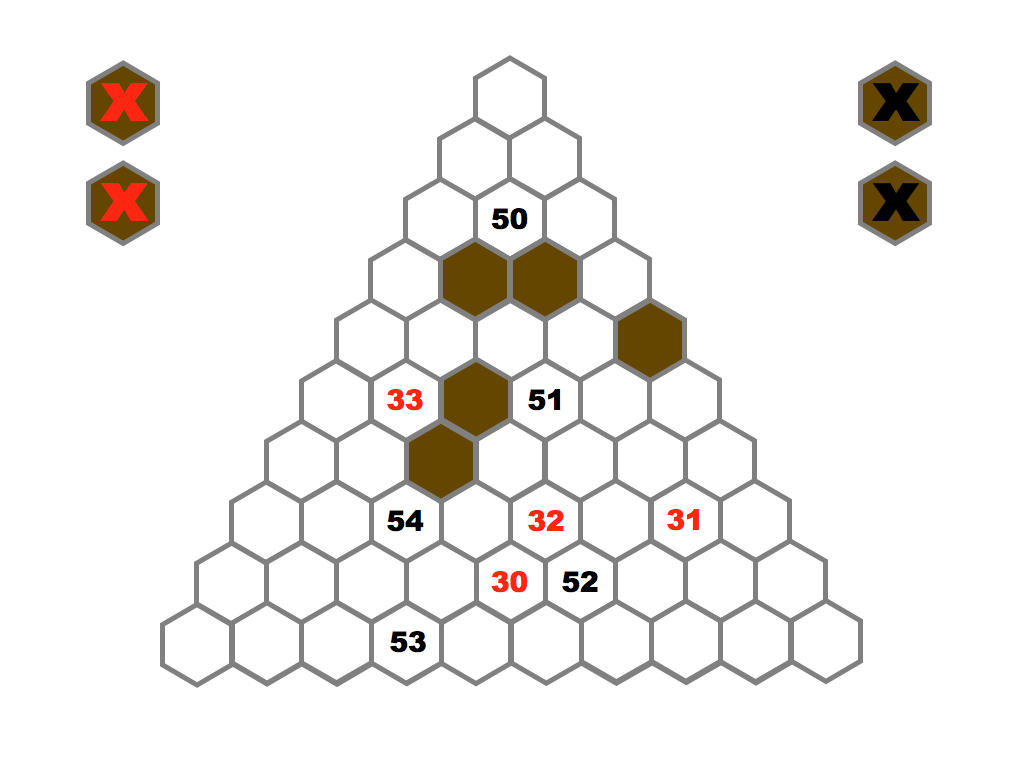
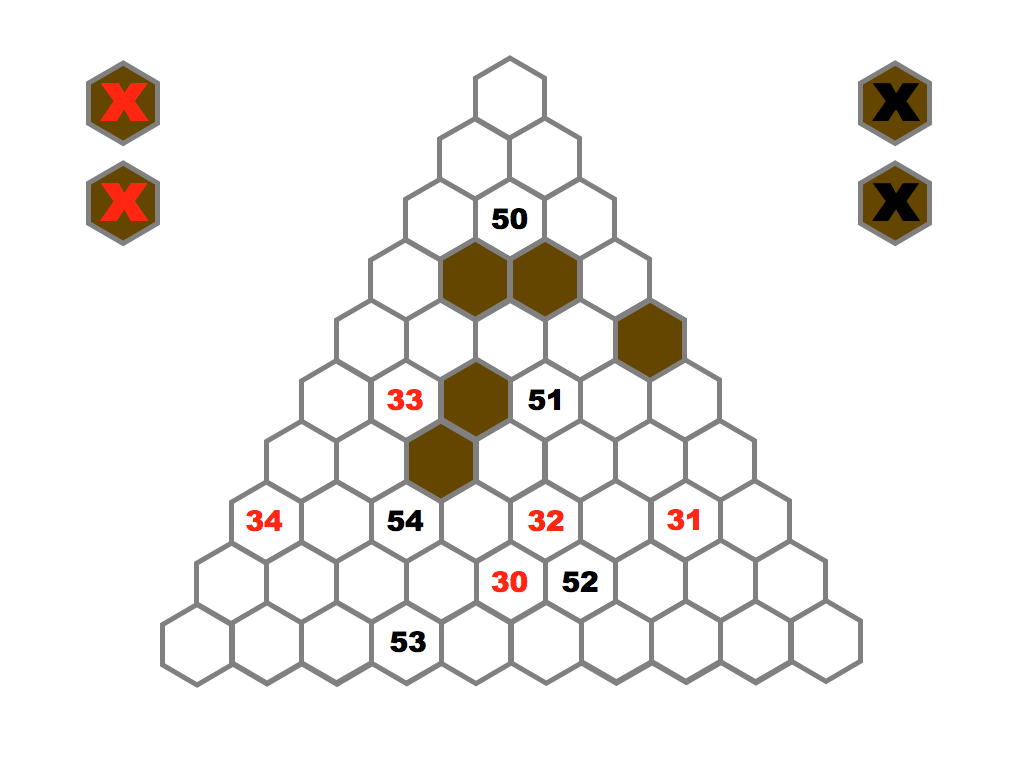
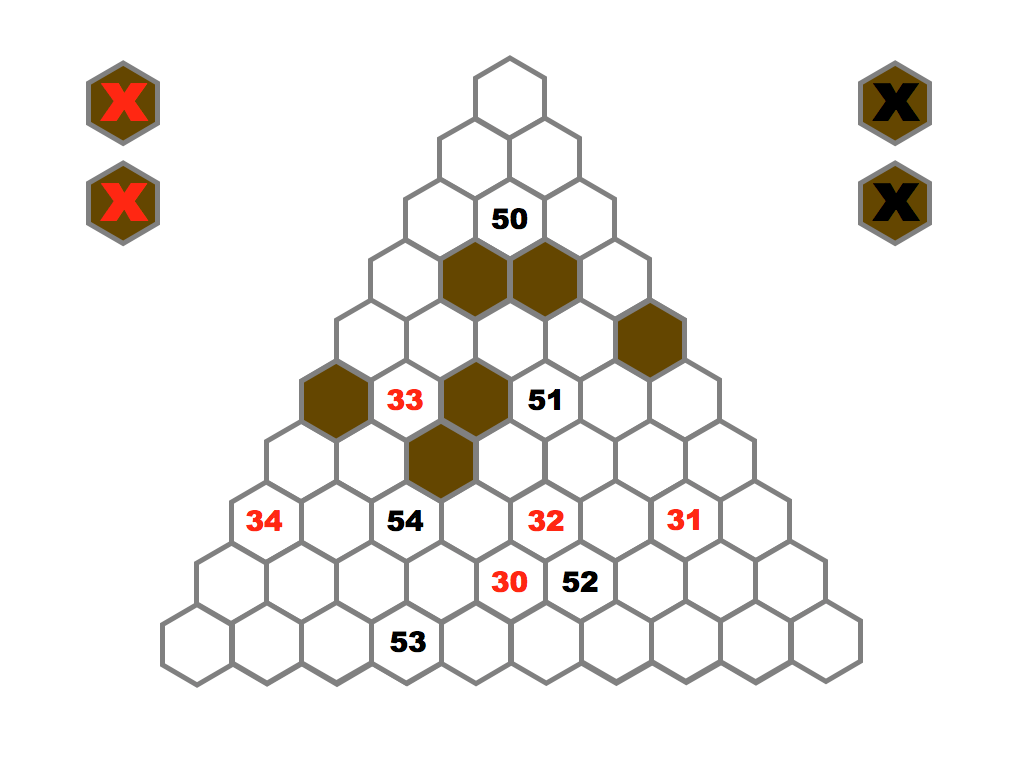
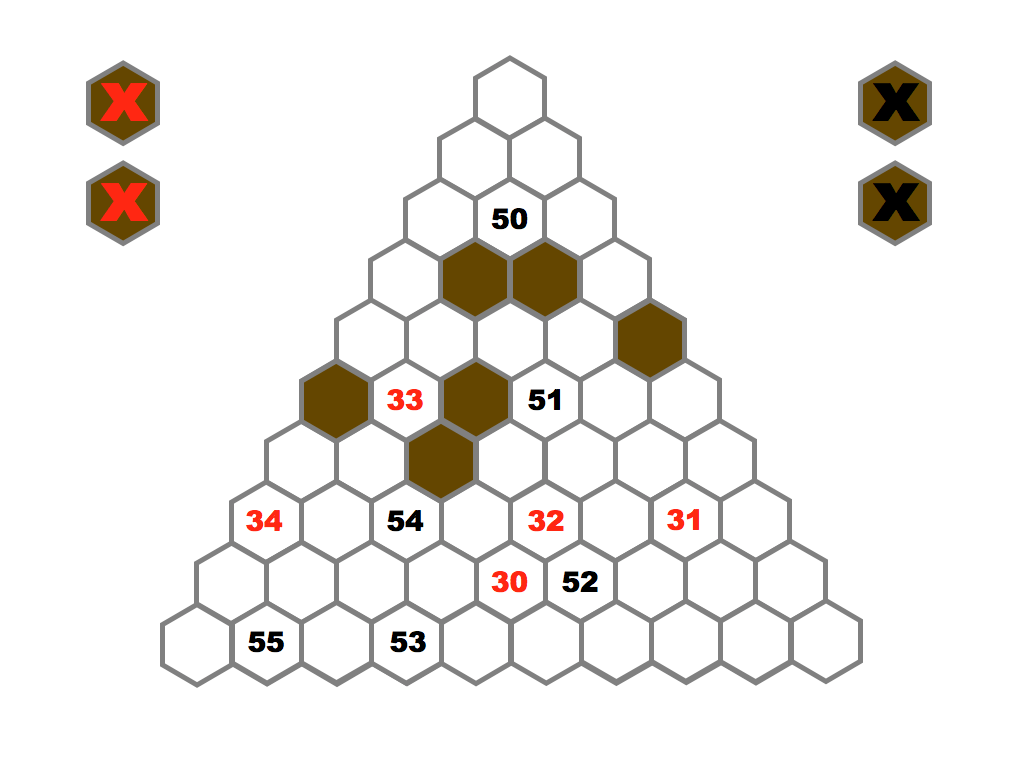
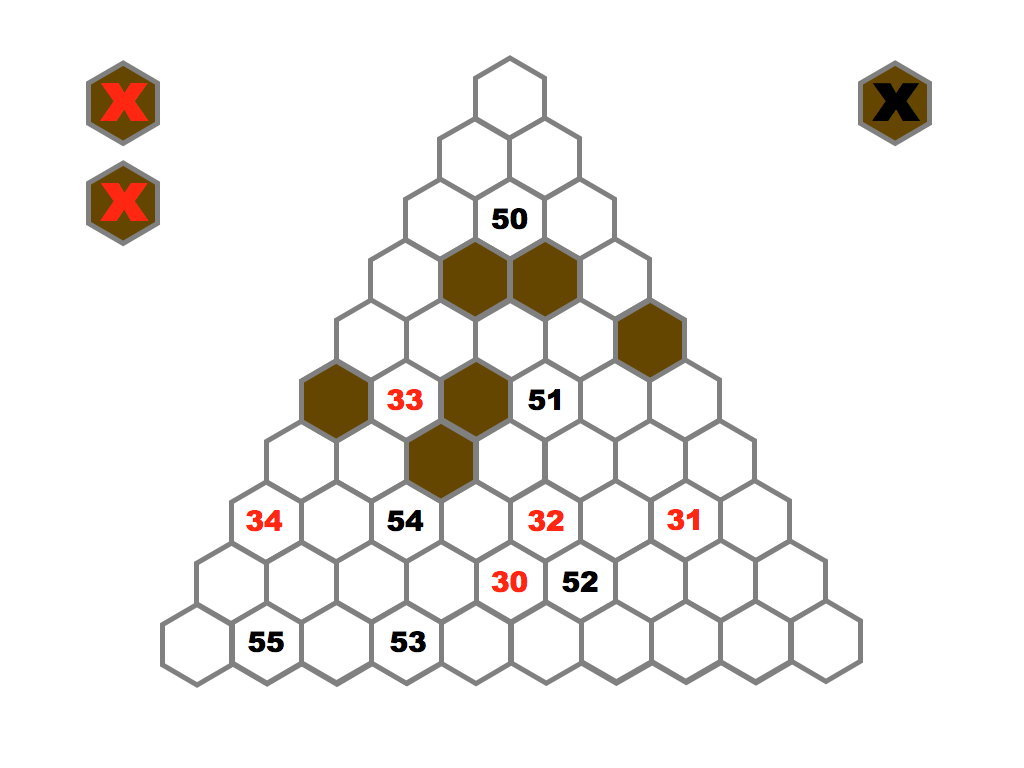
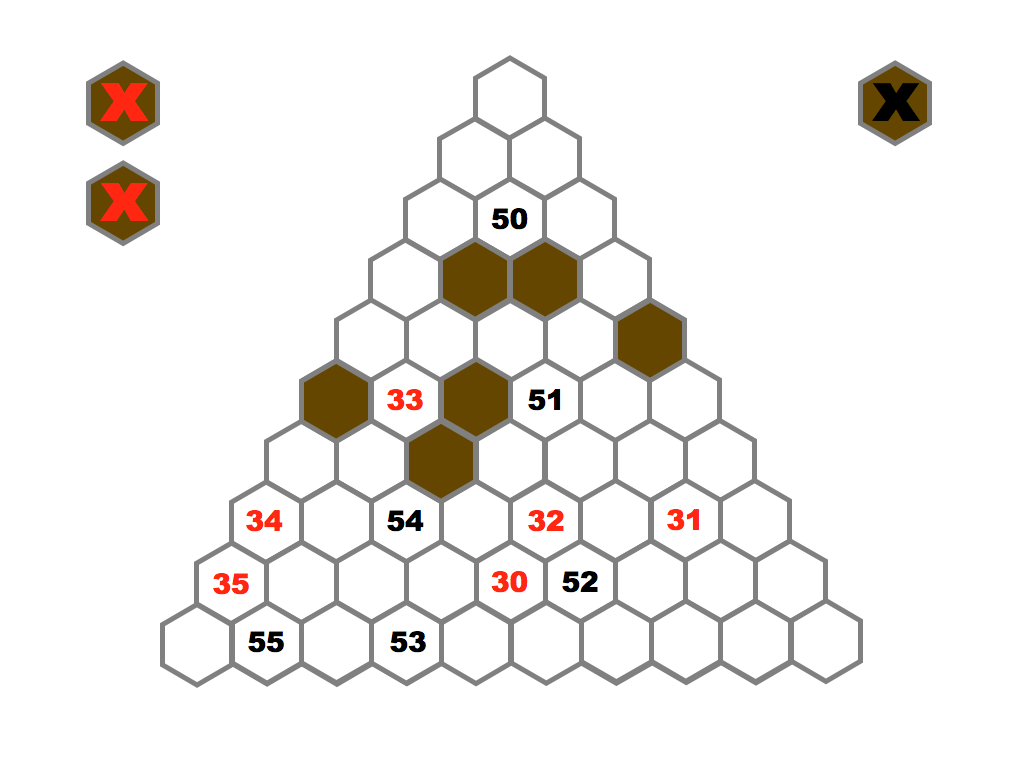
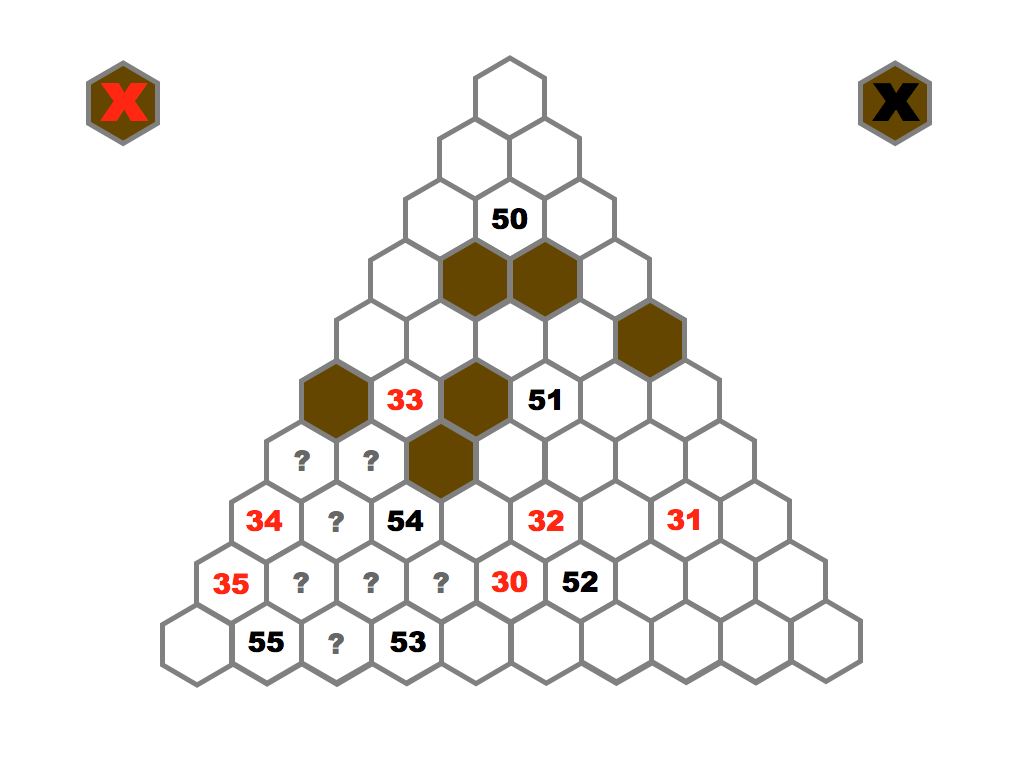
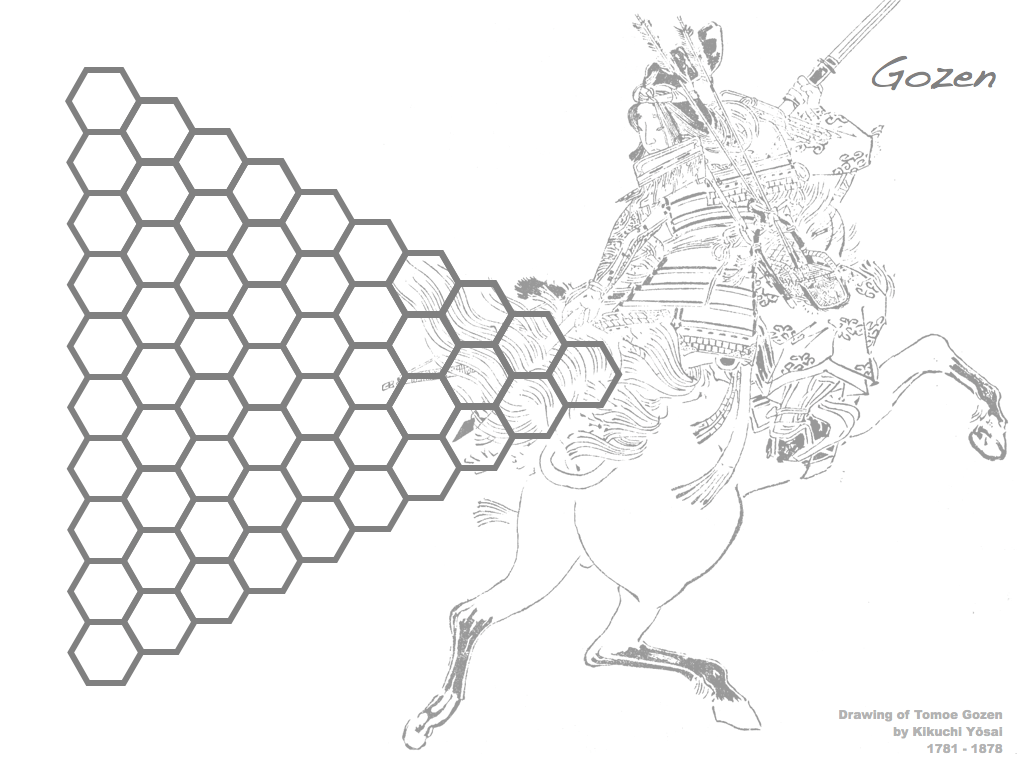
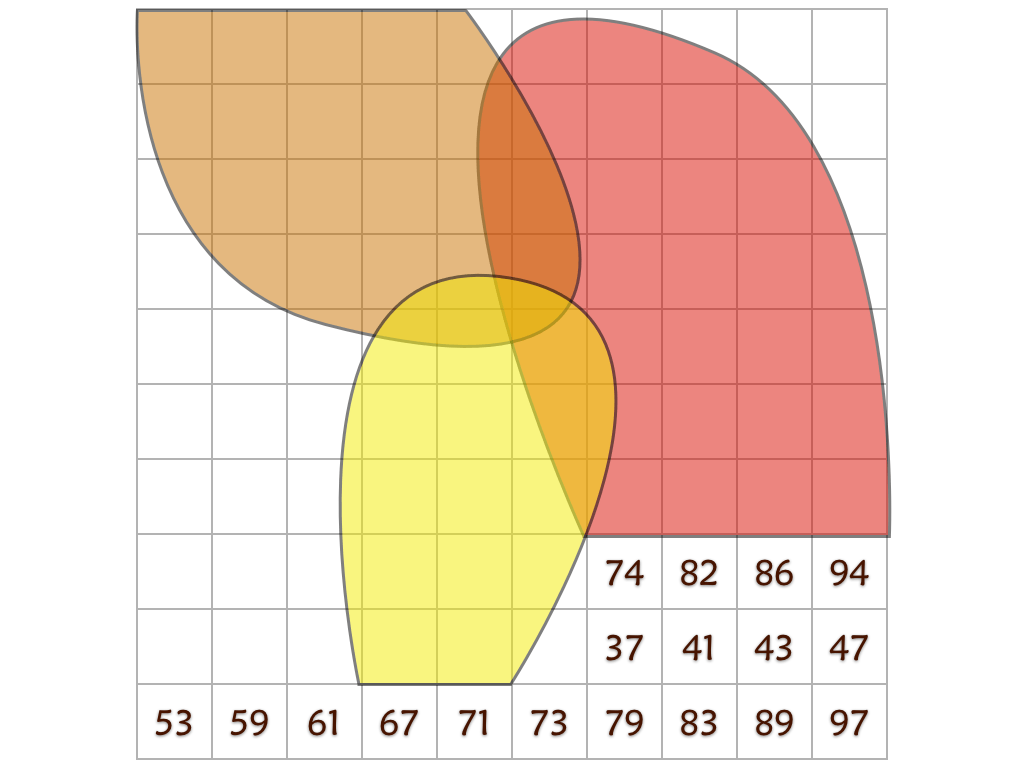
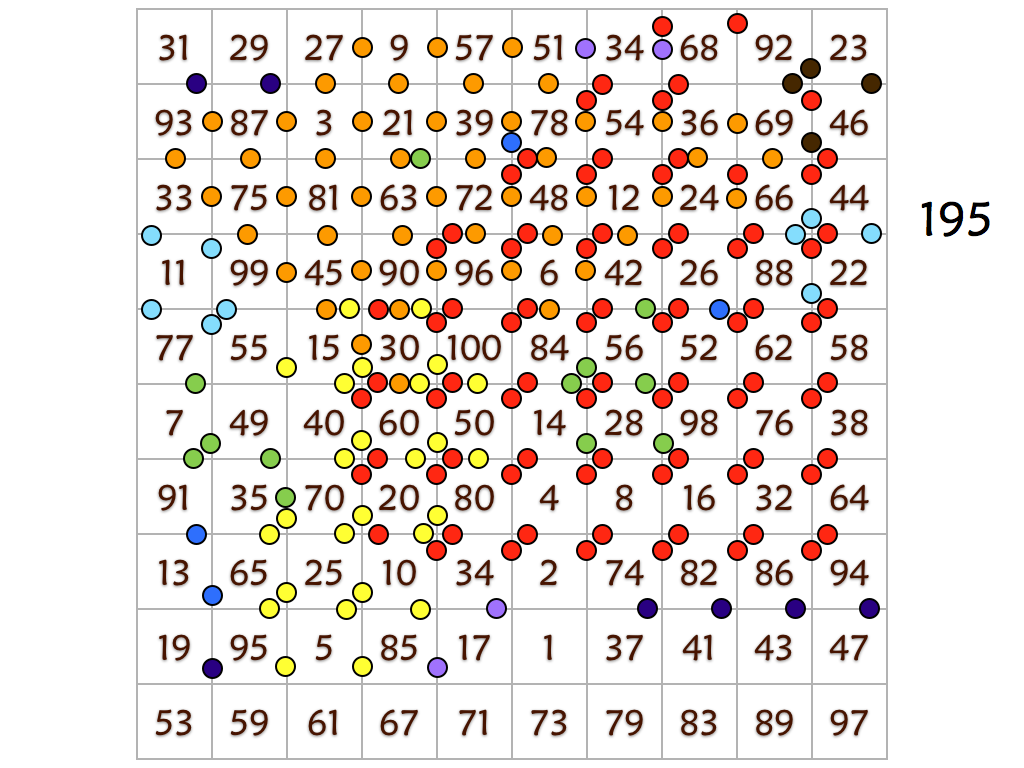
Several prime and composite numbers puzzles and mini-competitions. Rather than the hexagon shown in this video, the mimizu puzzles are best played on beautiful leaves that you can see and download in the slide presentation below.

This is a sequence developed by the great mathematician John Horton Conway.

After describing the sequence starting with 1,1 student pairs should start with their own two numbers from 1-10 and see what happens to their sequence. This is better than having all students work on the same sequence because then it just becomes a race and the slow, ponderous thinkers will feel justifiably uninspired. Do all sequences start doing the same thing?

Mimizu means earthworm in Japanese. Your goal is to digest leaves and other stuff that is in your compost bin. Number hints are given as well as black barriers which cannot be crossed.

After stepping through these slides click here to download printable mimizu puzzles.

You must eat all the leaf. This didn't work.

This is better because we ate through the whole leaf, but unfortunately there are other rules...

No Barrier Rule:

There must be no barrier between two numbers which share a common prime factor. 10 and 14 share a common prime factor of 2, so there should be no barrier between them. Our path is wrong.

Yes Barrier Rule:

There must be a barrier between two non-consecutive numbers which lack a common prime factor. 2 and 11 do not share a common prime factor, so there must be a barrier between them. Our path is wrong for a second reason.

Note:

Consecutive numbers never have a barrier between them.

Even though this path is wrong, there are some things which work. 9 and 15 have a common prime factor of 3. There must not be a barrier between them and indeed there is not. Good.

This is not an original puzzle, but it is one of my first experiences of a quality problem and therefore one that inspired my own designs. Here is the downloadable pdf.

The way I introduce Prime and Composite numbers is through one of the engaging puzzles above. However, most educators make the mistake of starting with a formal, but not quite as engaging, structuring of the subject matter.

Engage first – structure later.

If you absolutely feel compelled to introduce the structure first, then I suggest something like that shown in the video on the left where prime and composite numbers are introduced using elastic bands and talk of rectangles, square and line-segments.

This is absolutely one of my favourite pedagogic discoveries from recreational mathematics. It is engaging, evocative and curiosity inducing.

PS. Warning: This problem requires students to learn binary! Most curricula have this appearing years after students learn about prime number

Gozen - The 2-Player Pure Strategy Game

Gozen are female Samurai warriors. In this game your goal is to outlast your opponent by strategic horsemanship and archery.

After you view this slide show download game-boards here.

The battlefield may be any shape, but the standard game is on a triangular 10-board.

One player writes a black and red positive integer on two hexagons. The other player gets to choose to play black or red.

Black always moves first.

Each player gets three life which are the x markers flanking the game board. We will discuss them in a while, but first lets talk about horsemanship and archery.

Horsemanship

At the start of each turn you must ride 1-3 hexagons from your current location. Write the next highest integer in one of these hexagons. In this case the black player will write "51" somewhere in the green area.

Archery

Next it is time to shoot. You may shoot any hexagon on the board.

Black's turn is finished. It is now time for red's turn and to explain how you can lose.

Horsemanship

Red will write "31" in one of the green hexagons.

Losing the battle

If it were the end of Red's turn, Red would lose because...

Red's current location can see an enemy hexagon that does not share a common prime factor with itself. "50" and "31" do not share a common prime factor.

However, luckily for Red, it is not the end of Red's turn...

Red can still shoot an arrow.

Now it is the end of Red's turn, and thankfully red can no longer see the "50." It is only the closest number or destroyed hexagon that needs to be checked in each direction.

Black plays "52" - is that dangerous for black?

No - it is not dangerous. The "52" can see the "30" without danger because they share a common prime factor.

Black shoots an arrow.

Red makes a risky move and loses one of her three lives. Let's see why it is risky...

The move is risky because Red can see one of her own integers that does not share a common factor with her current number. "32" does not share a common factor with "31."

This check is made before shooting an arrow. If a risky move is made - the player loses a life and may not shoot an arrow that turn.

Red loses a life. If red loses all three, she has lost the game.

Is black's move risky?

Yes - Black's move was risky: "51" and "53" do not share a common prime factor. Black loses a life and does not get to shoot this turn.

Red's "33" does not see any of her own integers which are relatively prime. Actually she doesn't even see the "30" because a hexagon in-between has been destroyed.

Therefore - Red may shoot an arrow.

That is lucky, because if Red "33" saw Black "50" - Red would immediately lose because the two do not share a common prime factor.

Red saves the game by blocking the line-of-sight between her "33" and Black's "50."

Red does not have to worry about the 51. Why? Because both share a common prime factor of 3.

Black moves to "54."

Black shoots.

Red moves.

Red shoots.

Black makes a risky move...

Black loses a life and does not get to shoot this turn.

Red makes a risky move...

Red loses a life, but now it is Black's turn. Black has nowhere to go. Black loses.

The game board is the first page in this pdf file.

1-100 Composite Connector Challenge

This is a challenge for a class that has nothing to do except rejoice in connecting numbers that share common prime factors. The highest score that I've managed is 195, but I don't use computers so this can almost certainly be beaten. What I like about the challenge is that you can strategically think how to get a higher score.

Print out a 10 by 10 puzzle-sheet here - or just use standard graph paper. Then start adding the numbers 1-100. Here we have added 15 and 45. It is good that we have placed them together because they share a common prime factor.

We get 1 point because these neighbours share a common prime factor of 5.

We get an additional point because they also share a common prime factor of 3.

How many points do we get for adding the 60?

We get three points for the common prime factors of 2, 3, and 5 between 30 and 60.

Spoiler Alert: Do not keep going without trying this challenge.

I decided to start by grouping the big primes over 50 together at the bottom. I then decided to focus on getting an even region (red) a multiple of 3 region (orange) and a multiple of 5 region (yellow).

This was the best I did in an hour of play. I'm a mathematician so I don't expect too many of your students to come close, but the classroom discussion should get interesting. On the other hand, you may beat me 😉 That humiliation would be a joy to hear!