Event – Integer Sequences K-12

Integer Sequences K-12

Introduction to the Integer Sequences K-12 Conference

The On-Line Encyclopedia of Integer Sequences has many pedagogic gems that remain undiscovered by K-12 educators. These sequences need to be lifted out of obscurity and become a part of every child’s experience of mathematics.

The primary objective of this conference was to bring together educators and mathematicians to select 13 curricular integer sequences – one for each grade K-12. The secondary objective was to initiate a practical campaign to get the selected sequences the wide exposure they deserve.

It is not obvious that integer sequences – beyond those already in the curriculum – deserve pedagogic attention. It is easy to imagine their uninspired use in the classroom… for example: all students asked to independently reproduce a meaningless sequence term by term.

We didn’t let this happen. Our strength was in the collaboration between mathematicians (who can identify sequences that will reward a young explorer,) and educators (who know the curriculum and can predict classroom challenges.)

Sequence worthy of a full period (or more) of exploration need to engage students of diverse ability. Top students should be engaged because the sequence is intriguing and leads them to wonder, hypothesize and problem solve. Struggling students need to be engaged in acquiring curricular skills and problem solving.

The Online Encyclopedia of Integer Sequences posted the 13 selections here.

The text descriptions that follow are for mathematicians. The videos and slide shows are for teachers.

Kindergarten – A034326 Hours struck by a clock.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …

Grade 1 – A030227 Number of n-celled polyominoes with bilateral symmetry. (This description is for mathematicians – teachers can enjoy the leisurely slide show below)
1, 1, 2, 3, 6, 10, 20, 34, 70, 121, 250, 441, 912, 1630, 3375, …

Count the number of polyominoes with n squares that have mirror symmetry. There are 10. Grade one classes are capable of finding them all, but I’d start with an explanation that can be found on the following slides…

You might start like this: “Here are 13 squares. They form a shape that you might have seen before… Why is this shape special…”

The children will of course say that it is a letter of the alphabet…

“Yes, but that’s not why an Engineer or Butterfly Collector would find it special…”

“They would find it special because you can cut it in two…”

make a cutting action

“… and both sides are the same.”

“What about this shape?”

Pretending…

“This doesn’t look as good.”

Children urge you to change the direction of your cutting motion.

“Ah yes, you’re right…”

“What about this shape?”

Pretending…

“This looks like it should work…”

The children should protest.

“What about this one?”

Pretending…

“Surely, this has to work…”

The students will protest, and perhaps a few will do more than protest…

…and indicate a diagonal cut. Do not show them this diagonal until they have discovered it. You can pretend that you are the last person in the room to see it. Keep the illusion of first-time-discovery alive in your students 😉

“This looks better” you say. “I can see the cut.”

Here you are being purposefully misleading so your students can correct you. There is not ONE cut. There are many. Let your students correct you. Again, you pretend you are the last person in the class to be convinced that there is more than one right answer.

“So how many answers are there?”

There are four answers.

Now it is time to give pairs of students six squares and ask them to find all the possible shapes that they can create by putting the squares edge-to-edge. (Many students will make the mistake of trying to make a solution where half an edge touches another half edge. Stop the class and point out that this isn’t right for this puzzle.)

Throughout this exploration the shapes should be recorded permanently whenever they are discovered.

This is how I organized the ten results. On the left are those shapes with what I’ll call “horizontal or vertical” lines of mirror symmetry. On the right are those shapes with what I’ll call “diagonal” lines of symmetry.

If students are keen, you can repeat this activity on another day. This time with seven squares per group. Try this before you look at the next slide. I promise there are less than 25 to discover.

There are many questions that students may ask…

“Are there ever more shapes in the right circle?” (I do not know!)

“Can a shape go inside both circles?” (Yes, you already showed them one with 13 squares. Ask them to find one with 7 (impossible), 6 (impossible), 5 or less squares.

Everybody is collaborating. If a slow student discovers a shape that has already been discovered you follow your instinct to give that student what they need. Often this is not praise for working hard. We want students to internalize their joy at struggling to get an answer. Of course you never would praise a student for being smart. That language lessens resilience and tenacity.

Five squares give too few answers to make it my choice for a first day activity, but it is great for the third day… if you decide to delve into this problem that long.

Four squares…

Three squares…

Two squares…

One square…

So your class has shown that the total number of mirror-symmetric shapes increases as follows:

1 square: 1 shape… 2 squares: 1 shape…

3 squares: 2 shapes… 4 squares: 3 shapes…

5 squares: 6 shapes… 6 squares: 10 shapes…

7 squares: 20 shapes…

1, 1, 2, 3, 6, 10, 20…

It goes on… 34, 70, 121, 250, 441, 912, 1630, 3375… I like to call these big numbers “scary,” and you will likely see many students react with strong emotions when you quickly talk about these numbers. I know these are not curricular, but ONE sentence is great for your top students and you remove the stigma of math phobia by repeatedly exposing students to such terrors 😉

Now try this exercise with three Venn circles… adding a circle to indicate that the shapes inside have more than one line of mirror symmetry. Are all regions in this Venn diagram populated?

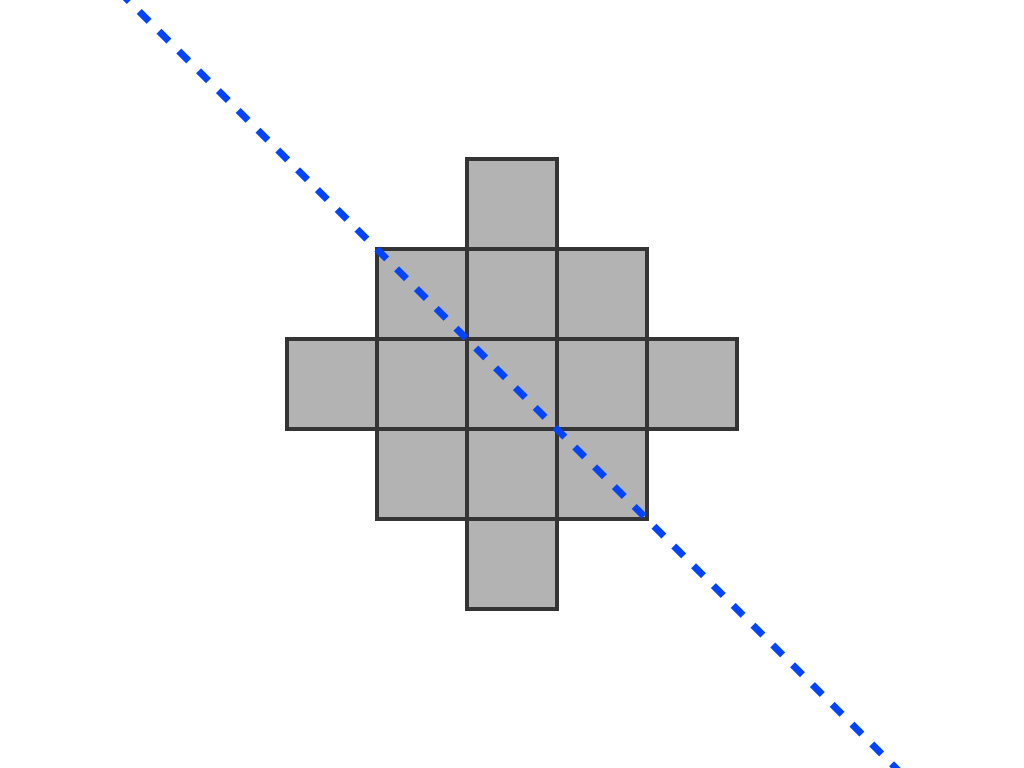
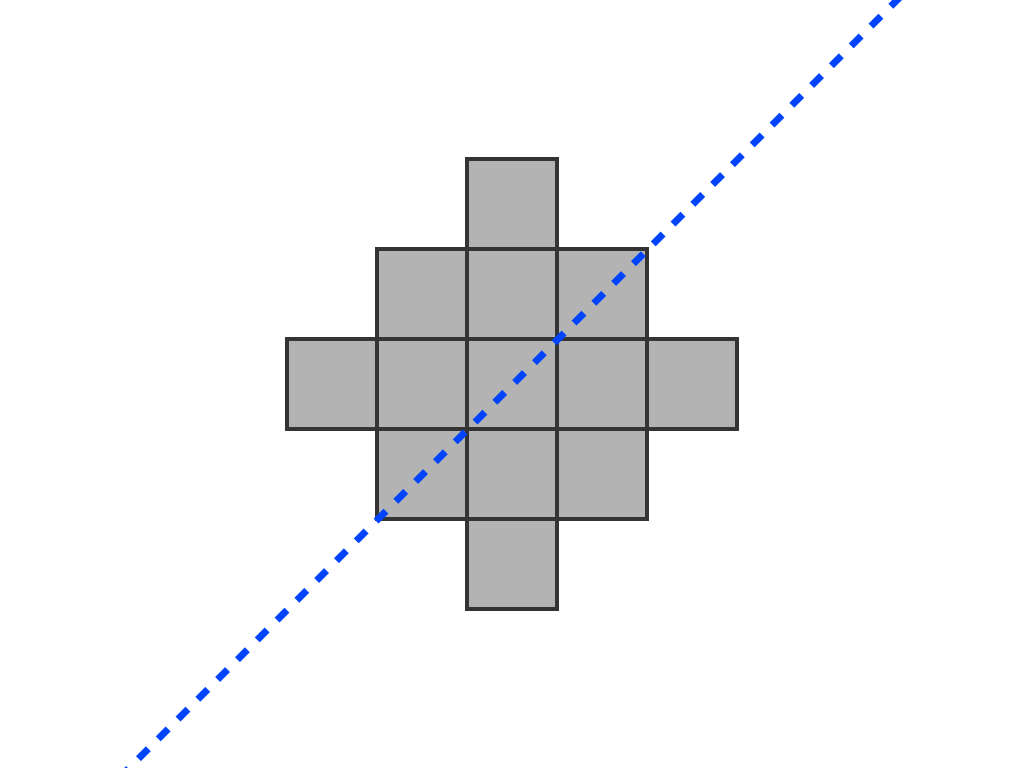
Grade 2 – A243205 – Consider the n X n Go board as a graph; remove i nodes and let j be the number of nodes in the largest connected subgraph remaining; then a(n) = minimum (i + j). (This description is for mathematicians)

1, 3, 5, 9, 12, 16, 20, 25, 29, 36?, 41?, 47?, …

This beautiful activity has now been made even more beautiful by using triangular grids rather than square grids. (see below)

Grade 3 – A254873 Recamán [division, -, +, *] – Starting at the seed number (14) the sequence continues by dividing, subtracting, adding or multiplying by the step number (2). Division gets precedence over subtraction which gets precedence over addition which gets precedence over multiplication. The new number must be a positive integer and not previously listed. The sequence terminates if this is impossible.

14, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, 24, 22, 11, 9, 18, 16, 32, 30, 15, 13, 26, 28, 56, 54, 27, 25, 23, 21, 19, 17, 34, 36, 38, 40, 20

(The above is for mathematicians. Teachers should view the slide presentation below.)

This Recaman-like sequence was discovered and explored by 15 year old Brian Kehrig from Renert School in Calgary. It is an intriguing exploration for students learning the four operations. Here is how it works.

Start by choosing:

1) a Starting Seed number

2) a Step number

In this example we’ll choose our Starting Seed number as 14 and our Step as 2.

To find the next term ask if the current number can be divided by the Step number. The resulting number must be a positive integer not already in the sequence.

If this is impossible – go on to subtraction. Try subtracting the Step number. If this is impossible – go on to addition. If this is impossible – go on to multiplication.

In this case we can use division… so our next term will be 14 / 2 = 7.

To find the next term we cannot use division since 7 divided by the step number is not a positive integer.

We can use subtraction. 7 – 2 = 5.

Again, we can’t use division, but we can use subtraction so the next term will be 5 – 2 = 3.

Again, we cannot use division, so our next term is 3 – 2 = 1

We cannot use division.

We cannot use subtraction (we need a positive integer.)

We cannot use addition (1 + 2 = 3 is already in the sequence.

Our last chance is to use multiplication. If this fails, the sequence terminates. Luckily, multiplication works: 1 x 2 = 2.

We cannot use division.

We cannot use subtraction (we have already visited 1.)

We can use addition (2 + 2 = 4.)

We can keep going like this for a little bit of time before something interesting happens. Try it. It should take you ten minutes at most…

Spoiler… next slide shows what happens…

It just stops. Once we get to 20 there is nowhere for this sequence to go.

With step 2, this is the first time this happens. Please do NOT start with Step 2 and Starting Seed 14. Let the students explore smaller Seeds first and have this as a cool discovery mid-way through the class.

Results should be plotted at the front of the class…

I’ve put a “T” for terminated, but your students might want to record more detailed information… like the highest number attained or the number of terms in the sequence when it terminated.

Next I’ll show you a more typical sequence…

With a Starting Seed of 10 and a Step of 2, the sequence does not terminates, but slowly climbs to infinity. The student or pair of students who discover this should record their result…

Here, I’ve just put an infinity sign, but perhaps your students would be more creative and add something about the sequence’s behaviour before it started its climb. For example, they might write the term at which the sequence starts its perpetual rise.

Grade 4

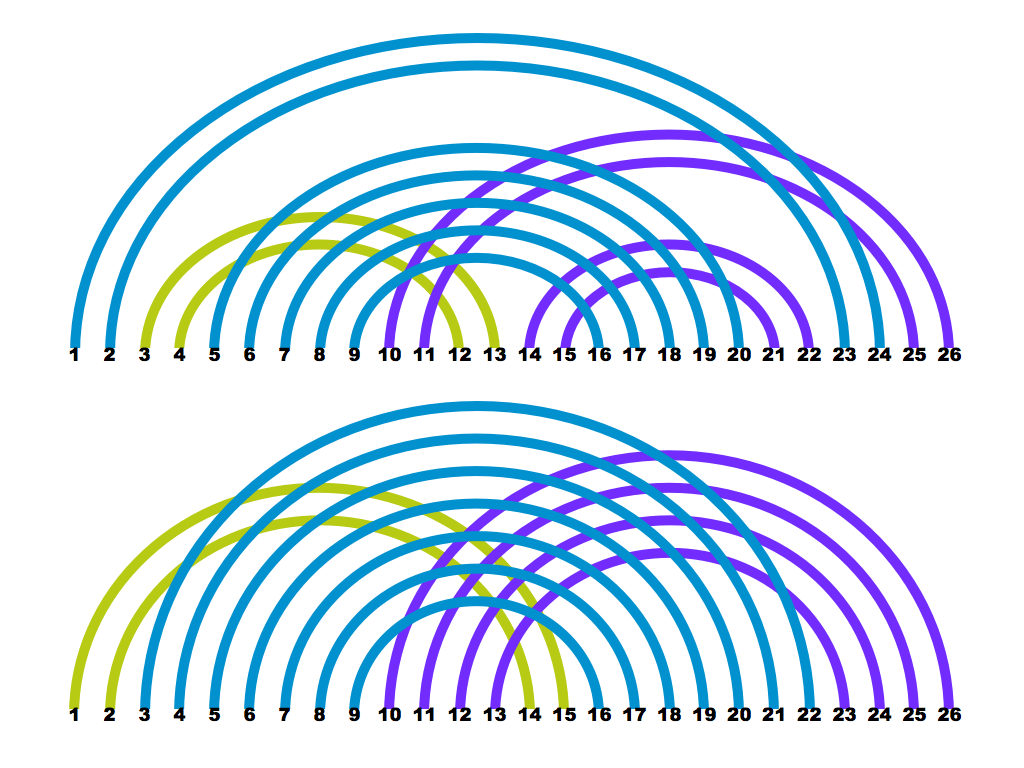
A253472 Numbers n such that 1, 2, …, 2n can be partitioned into n pairs, where each pair adds up to a perfect square.

4, 7, 8, 9, 12, 13, 14, 15, 16, …

(The above is for mathematicians. Teachers should view the slide presentation below.)

Rainbow Squares is a challenge inspired by Henri Picciotto. Each rainbow arc needs to be anchored at two integers that sum to a square. Here we have tried to find a solution for 1-10, but have failed because the last two numbers, 2 and 3, do not sum to a square. Is this possible?

Downloadable Rainbow Square puzzle-sheets here.

1-10 did not work. It was impossible. However, 1-26 does work. Complete the two puzzles on the left. Spoiler alert: the next page will give the answers.

Solution to the previous slide.

Another pair of puzzles with the solution on the next page...

Solution to the previous slide.

Here I've failed with 1-60 because the remaining numbers, 21 and 22, do not add to a square. Even though there are over 4 million solutions to this it took me more than an hour to find one! Computers are reliably good at these kind of brute force searches. I choose not to tell students how good computers are because everyone wants to feel awesome when they solve something difficult - not be told that a computer found 4 million solutions in one second. It is a matter of our human pride 😉

Grade 5

A256174 Boomerang Fractions – Starting with 1, on the first step add 1/n, and on subsequent steps either add 1/n or take the reciprocal. a(n) = number of steps required to return to 1. (The sequence starts with a(2).)

4, 9, 7, 20, 6, 33, 13, 23, 16, 62?, 8, 75?, 18, 17, 25, …

(The above is for mathematicians. Teachers should stay tuned 😉

Grade 6

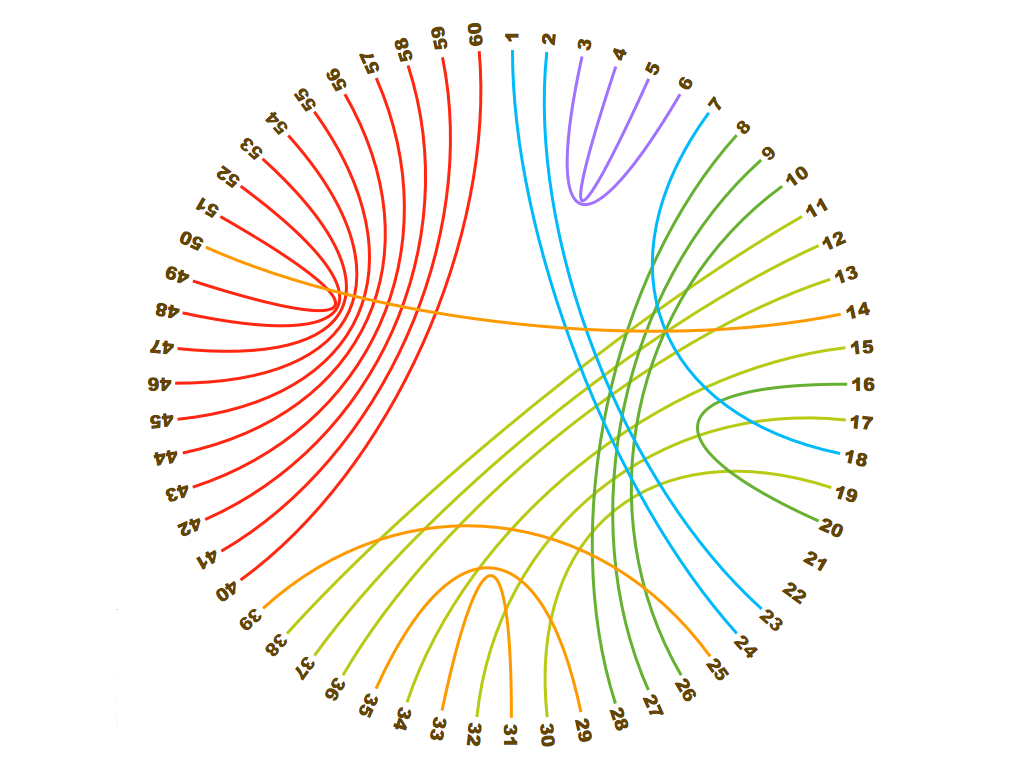
A125508 Integral Fission – A prime factorization tree in which every pair of children is chosen so they are as equal as possible and the largest child goes on the right. a(n) are the lowest numbers for which a new tree shape is encountered.

2, 4, 8, 16, 20, 32, 40, 64, 72, 88, 128, 160, 176, 200, 220, 256, 272, 288, 320, 336, 360, 400, 420, 460, 480, 512, 540, 544, 640, 704, 864, 880, 920, …

(The above is for mathematicians. Teachers should view the slide presentation below.)

Integral fission is a variant of prime factorization trees allows the creation of a treasure trove of puzzles. The newest puzzle is to find the first time each Integral Fission shape is encountered. Download the Puzzle-sheet, instructions and solutions here.

Grade 7

A039834 Fibonacci numbers (A000045) extended to negative indices. F(0) = 0 in the sequence below.

1, 1, 0, 1, -1, 2, -3, 5, -8, 13, -21, 34, -55, 89, -144, …

Grade 8

Similar to A226595 … but actually “Lengths of maximal non touching increasing paths in n X n grids starting at the upper left and ending at the lower right.”

0, 2, 4, 6, 9, 12?, 15?, 17?, 20, …

(This is for mathematicians. Teachers should watch the first part of the video below.)

Grade 9

A069283 The number of ways that n can be written as the sum of at least two consecutive positive integers.

0, 0, 0, 1, 0, 1, 1, 1, 0, 2, 1, 1, 1, 1, 1, 3, 0, 1, 2, 1, 1, 3, 1, 1, 1, 2, 1, 3, 1, 1, 3, 1, 0, 3, 1, 3, 2, 1, 1, 3, 1, 1, 3, 1, 1, 5, …

Grade 10

A225745 Smallest k such that n numbers can be picked in {1,…,k} with no four in arithmetic progression.

1, 2, 3, 5, 6, 8, 9, 10, 13, 15, 17, 19, 21, 23, 25, 27, 28, 30, 33, 34, 37, 40, …

Grade 11

A000108 Catalan numbers: C(n) = binomial(2n,n)/(n+1) = (2n)!/(n!(n+1)!).

1, 1, 2, 5, 14, 42, 132, 429, 1430, …

Grade 12

A000127 Maximal number of regions obtained by joining n points around a circle by straight lines. Also number of regions in 4-space formed by n-1 hyperplanes.

1, 2, 4, 8, 16, 31, 57, 99, 163, 256, …

Here are videos taken during the conference:

My opening address and ideas about how to choose integer sequences for the classroom.
Henri Piccotto talks about some sequences.
My mentor, Richard Guy (at age 98) talk#1 and talk#2.