by MathPickle | Sep 19, 2015 |
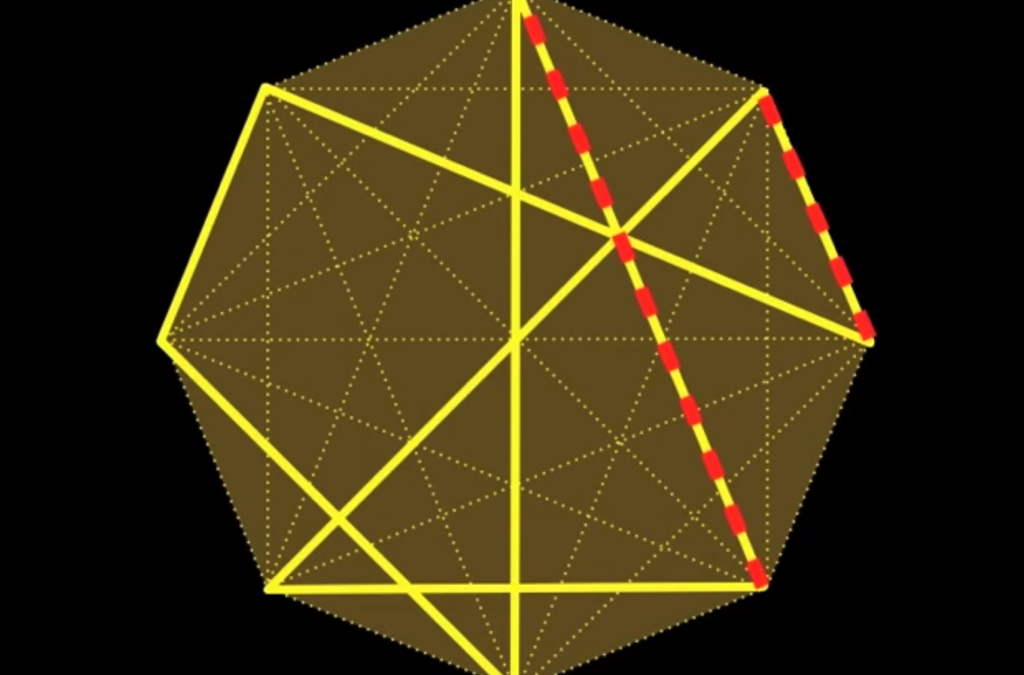
Parallel Lines and Slopes (MathPickle, 2010) Introduce parallel lines through this beautiful puzzle. Is it even possible? If a solution does exist it is certainly difficult to find, but no promises that a solution actually exists. The other puzzles are good to get...

by MathPickle | Sep 19, 2015 |
64 = 65 Mathemagical Proof (Martin Gardner) Get your older students to break apart a convincing mathemagical trick by linking it to the Fibonacci sequence and calculating the slopes of some line segments. Younger students derive a lot of pleasure by figuring out that...
by MathPickle | Sep 19, 2015 |
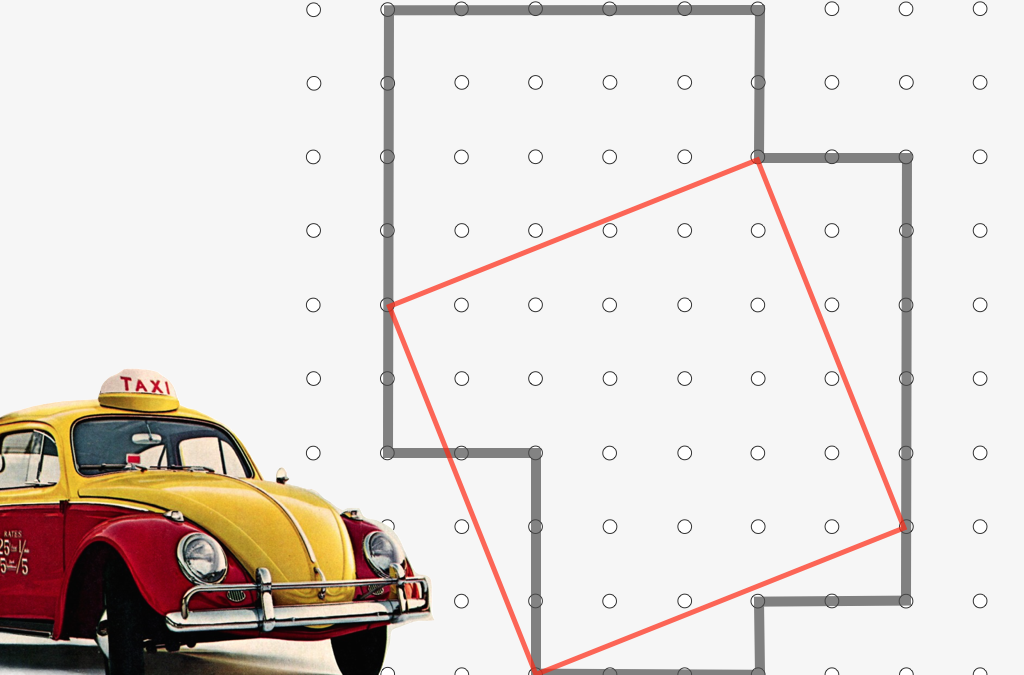
Taxi Cab Squares (inspired by the Inscribed square problem of Otto Toeplitz, 1911) Give your students practice with Cartesian coordinates as they explore a new variant of a famous, unsolved problem of Otto Toeplitz (1911). This problem has a very wide spectrum of...

by MathPickle | Sep 18, 2015 |
Scientific Notation Notrivia (MathPickle, 2010) Practice Scientific Notation with in a trivia game. Each question will ask you to place an unknown length in relationship to two other known lengths. Have a mini-competition in class... The game on the left is where you...
by MathPickle | Sep 18, 2015 |
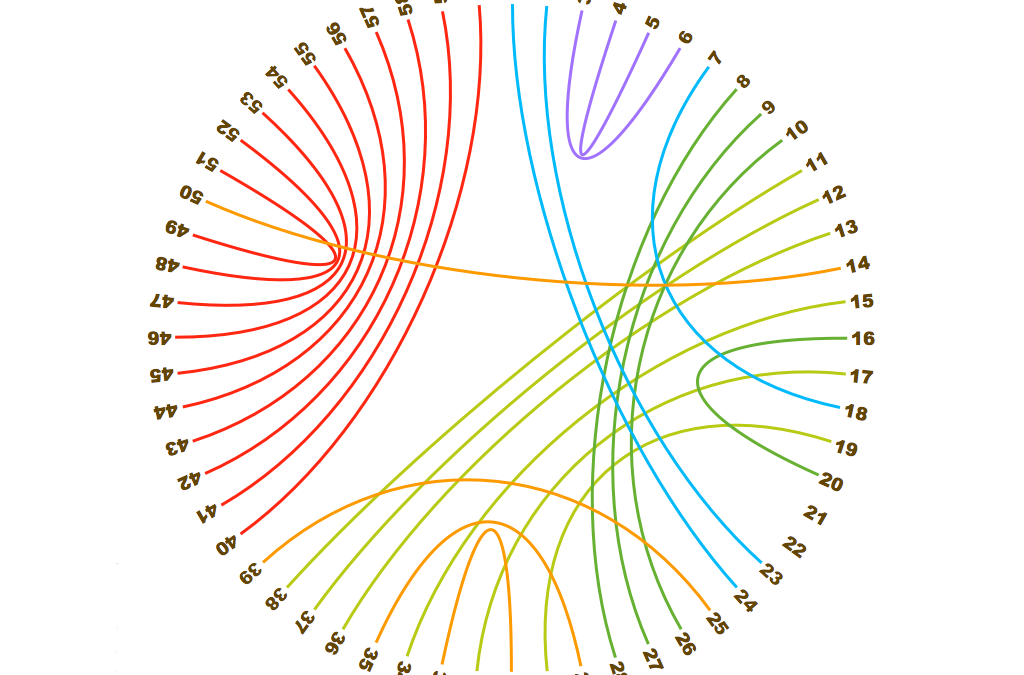
Rainbow Squares is a challenge inspired by Henri Picciotto. Each rainbow arc needs to be anchored at two integers that sum to a square. Here we have tried to find a solution for 1-10, but have failed because the last two numbers, 2 and 3, do not sum to a square. Is...





