by MathPickle | Sep 19, 2015 |
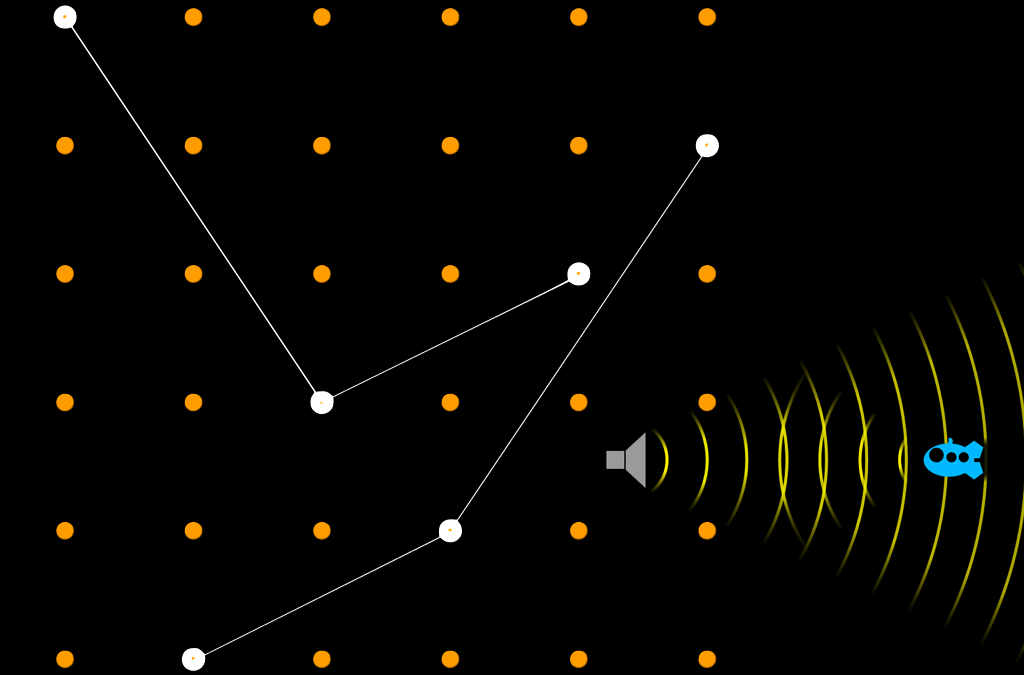
Hunting Submarines (John Costas, 1965) Costas arrays were part of submarine warfare and a great way to get practice with slopes. It is an unsolved problem of mathematics whether a Costas array exists for all nxn squares. The smallest square for which no answer is...
by MathPickle | Sep 19, 2015 |
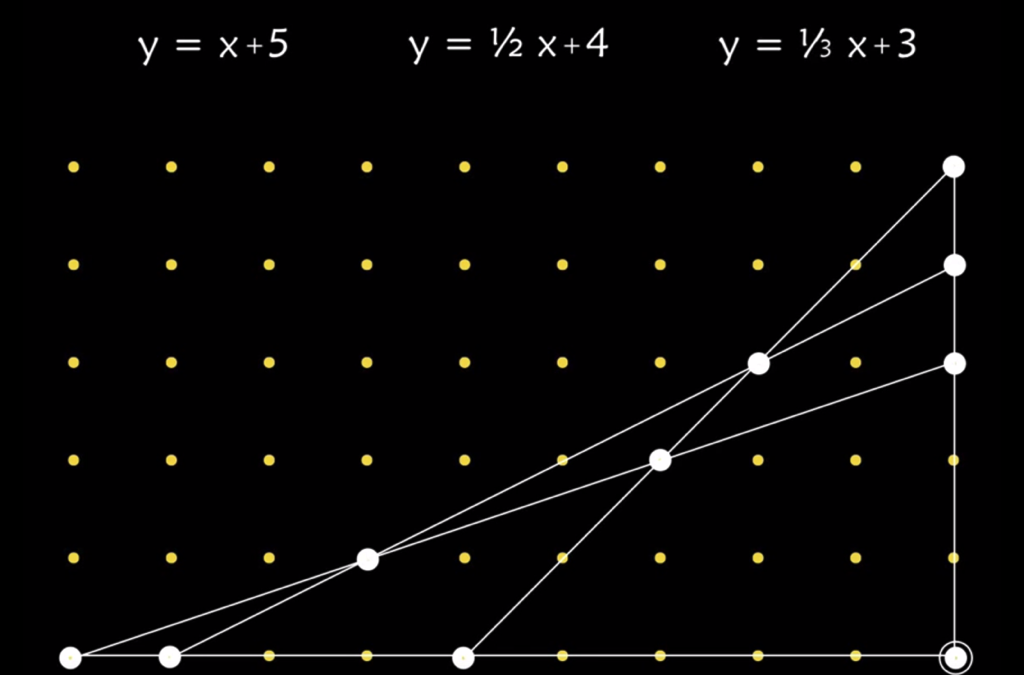
10 Points, 5 Lines, 4 Points on each Line (Henry Dudeney, 1917) Play with lines in a Cartesian coordinate system in this 1917 puzzle by the great puzzle-master Henry Dudeney. We must say that there are as many squares as there are numbers. Galileo Galilei Join the...
by MathPickle | Sep 19, 2015 |
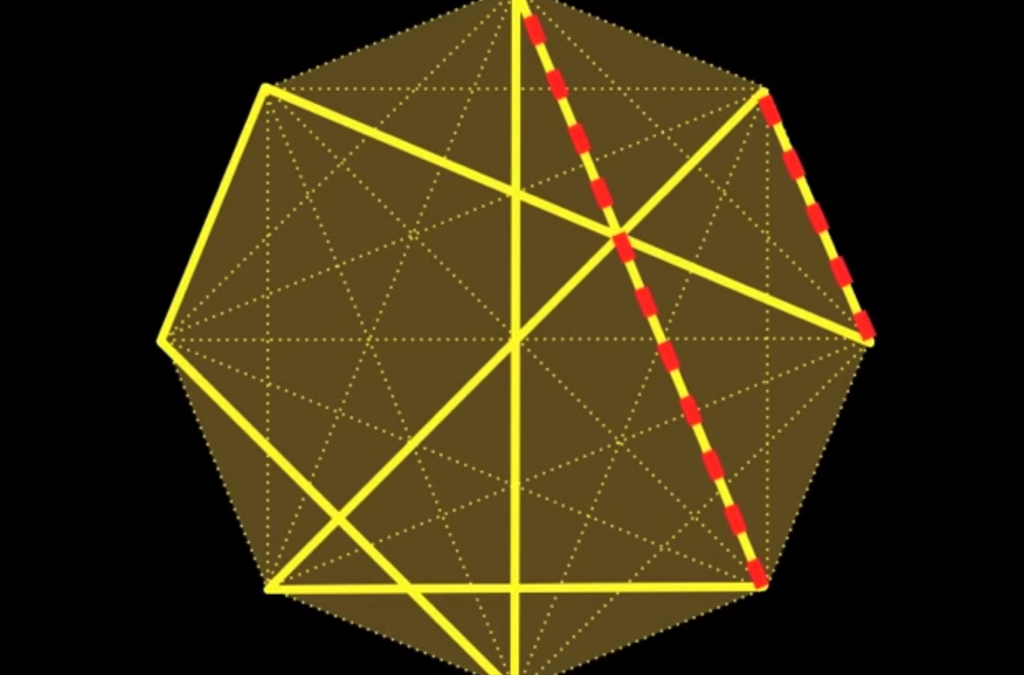
Parallel Lines and Slopes (MathPickle, 2010) Introduce parallel lines through this beautiful puzzle. Is it even possible? If a solution does exist it is certainly difficult to find, but no promises that a solution actually exists. The other puzzles are good to get...

by MathPickle | Sep 19, 2015 |
64 = 65 Mathemagical Proof (Martin Gardner) Get your older students to break apart a convincing mathemagical trick by linking it to the Fibonacci sequence and calculating the slopes of some line segments. Younger students derive a lot of pleasure by figuring out that...
by MathPickle | Sep 19, 2015 |
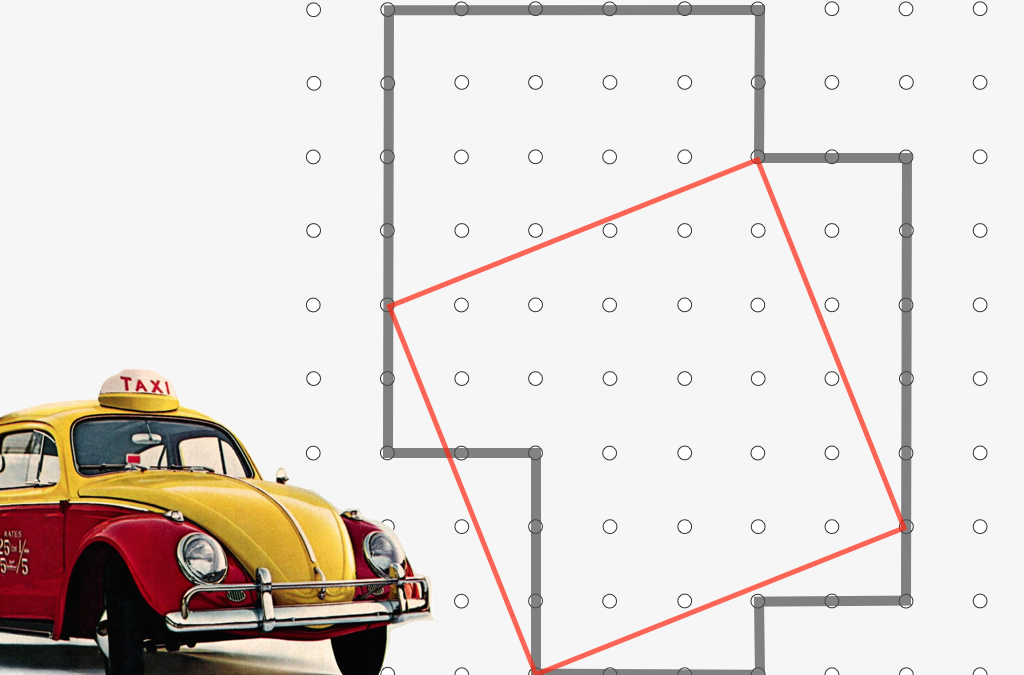
Taxi Cab Squares (inspired by the Inscribed square problem of Otto Toeplitz, 1911) Give your students practice with Cartesian coordinates as they explore a new variant of a famous, unsolved problem of Otto Toeplitz (1911). This problem has a very wide spectrum of...





