
by MathPickle | Nov 28, 2016 |
Uncracked 114 (Diophantus of Alexandria, c. 215-290) Students working with exponents should be asked to find which values of n from 0-100 are possible by summing the cubes of three positive integers: a^3 + b^3 + c^3 = n. Next, ask if the cubes can be negative. This is...

by MathPickle | Oct 29, 2016 |
The Josephus Problem (Josephus, 1st Century) This is a great and accessible proof whose basis in historic violence is sure to appeal to that half of the class with too much testosterone. Search for: Recent Posts How to pair up students? A Message to Mathematicians...

by MathPickle | Oct 8, 2016 |
Celtic Counting requires students to trace an under and over pattern – counting the Celtic loops. How many loops exist in this knot? There are two. How many loops does this knot have? There are three. The following slides have larger knots, but students age 6+...

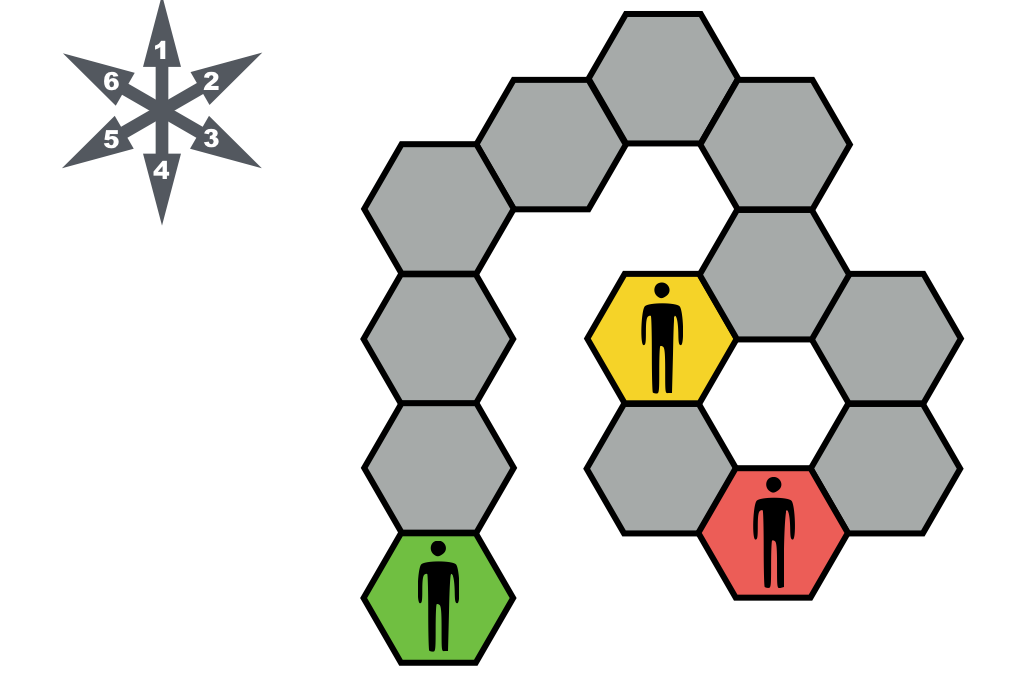
by MathPickle | Aug 12, 2016 |
Imagine a spider going for a morning walk around the web. At each intersection he rolls a dice (carefully so it doesn’t stick) to determine the next direction. If the dice point him towards an intersection already visited – he rolls again. How...
by MathPickle | Jun 21, 2016 |
Richard Smalley was awarded the Nobel prize in Chemistry for the discovery that he could make a very very small soccer ball out of Carbon atoms. In 2005 he suddenly began to shrink. He ended up so small that he could bounce on the little trampolines that make...





