
by MathPickle | Sep 16, 2015 |
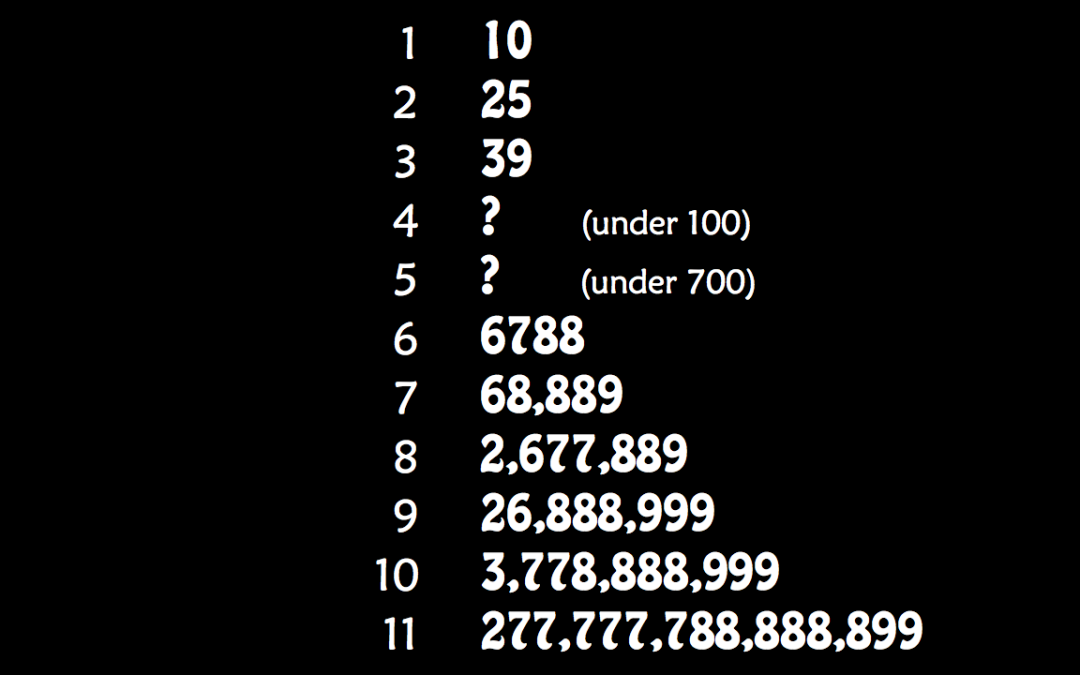
Toothpick, Vampire and Domino Sequences (Clifford Pickover, 1994) Recreational mathematics is on the fringes of mathematics, but its real worth is in mathematical pedagogy. Vampire Numbers are a perfect example. They are ridiculous. Most mathematicians would not take...
by MathPickle | Sep 16, 2015 |
Multiplicative Persistence (Gottlieb, 1969) The persistence of an integer is the number of times you can perform the following before ending up at a single digit: 1) Take the digits of the integer and multiply them together to give a new integer. 2) Repeat #1 using...
by MathPickle | Sep 16, 2015 |
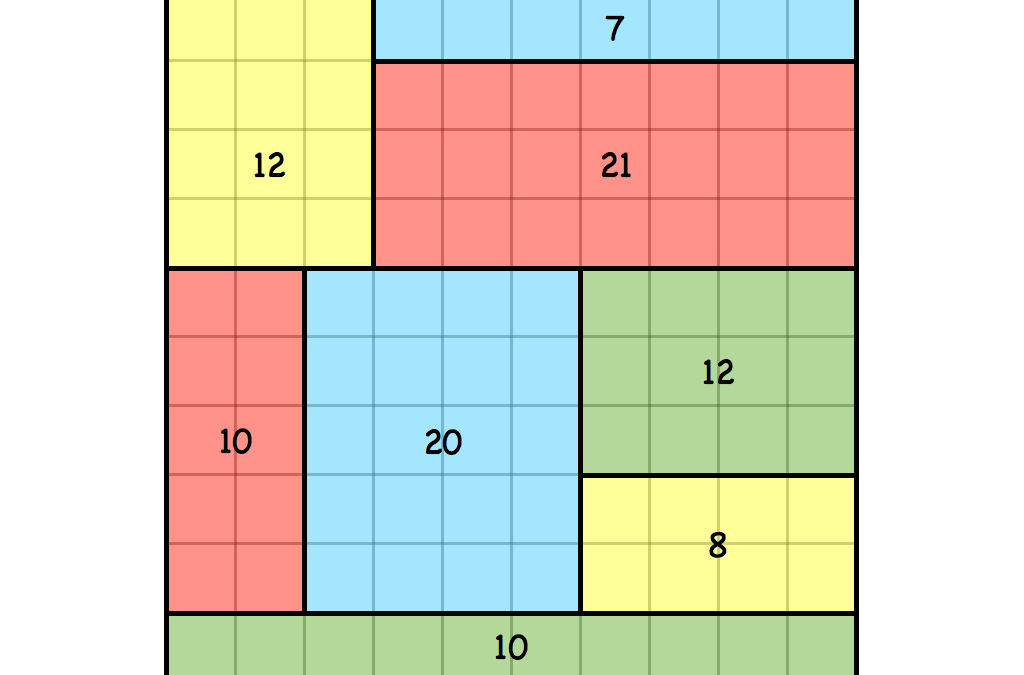
Mondrian Art Puzzles People who gaze upon a piece of Mondrian art should ask how he decided which colors to paint where. The disgruntled person may even ask what the piece of artwork might have looked like if Mondrian had taken the time to color it all in… In...

by MathPickle | Sep 15, 2015 |
Beetle Blitz! (MathPickle, 2013) We learn best through hard fun. These games are for students who need practice with single digit multiplication. They are entirely unfair – almost always one beetle will have a winning strategy. I love to emphasize this to help...
by MathPickle | Sep 15, 2015 |
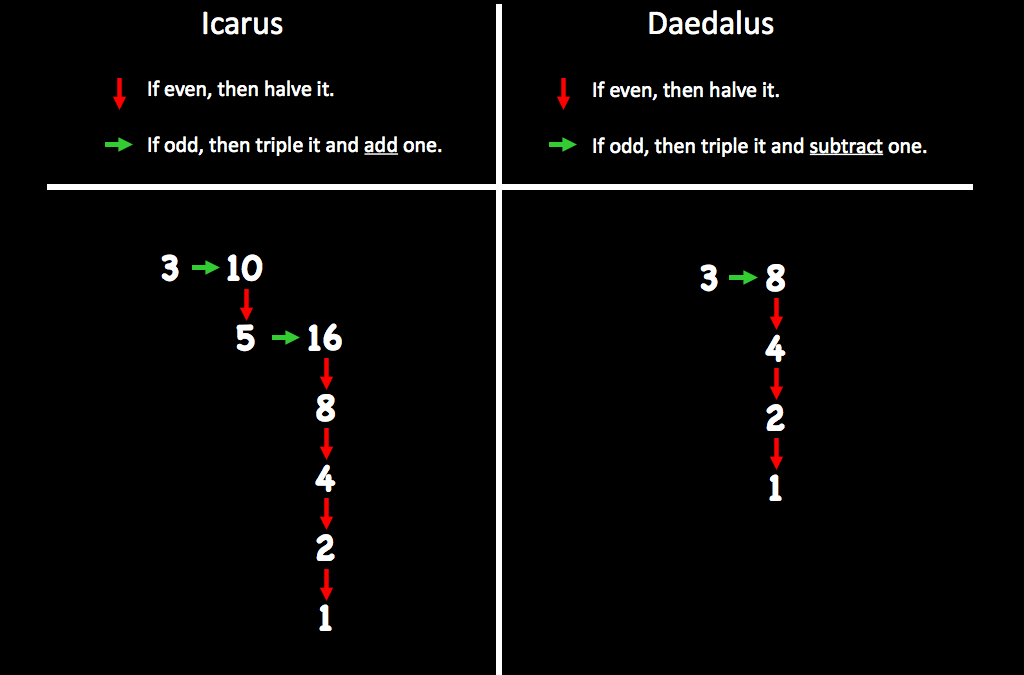
Daedalus and Icarus try to Escape (Lothar Collatz, 1937) The Collatz conjecture from 1937 is essential in every student’s experience of mathematics. Here we present it with a backdrop from Greek mythology. It gives students practice in multiplying by 3 so when the...





