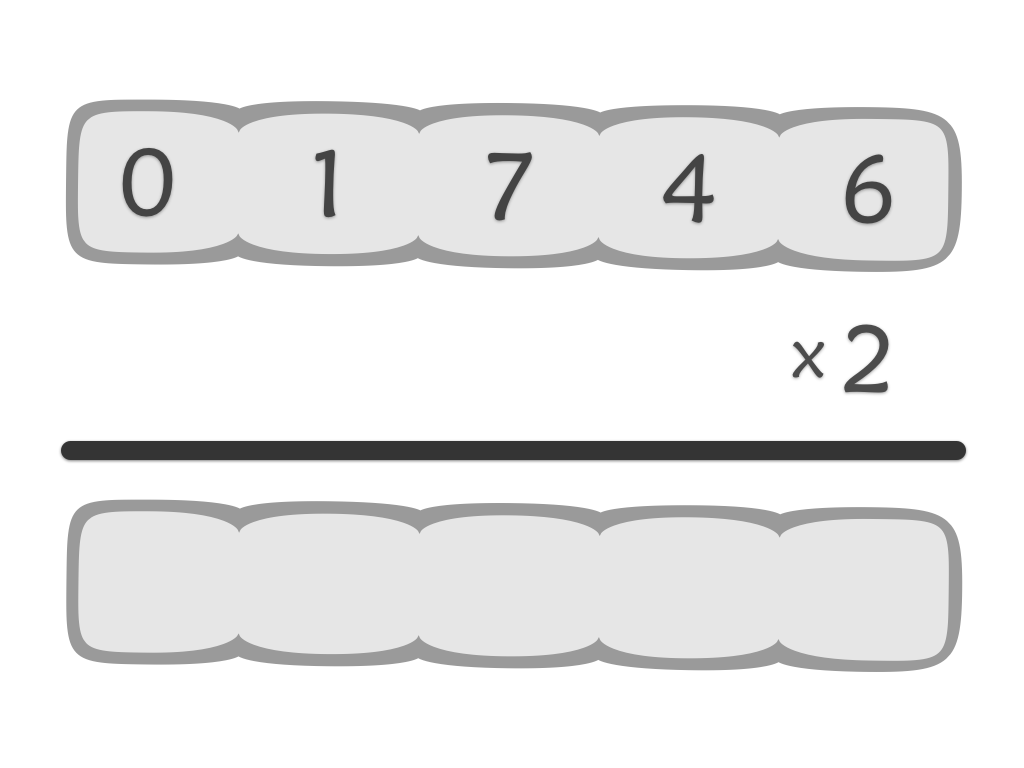
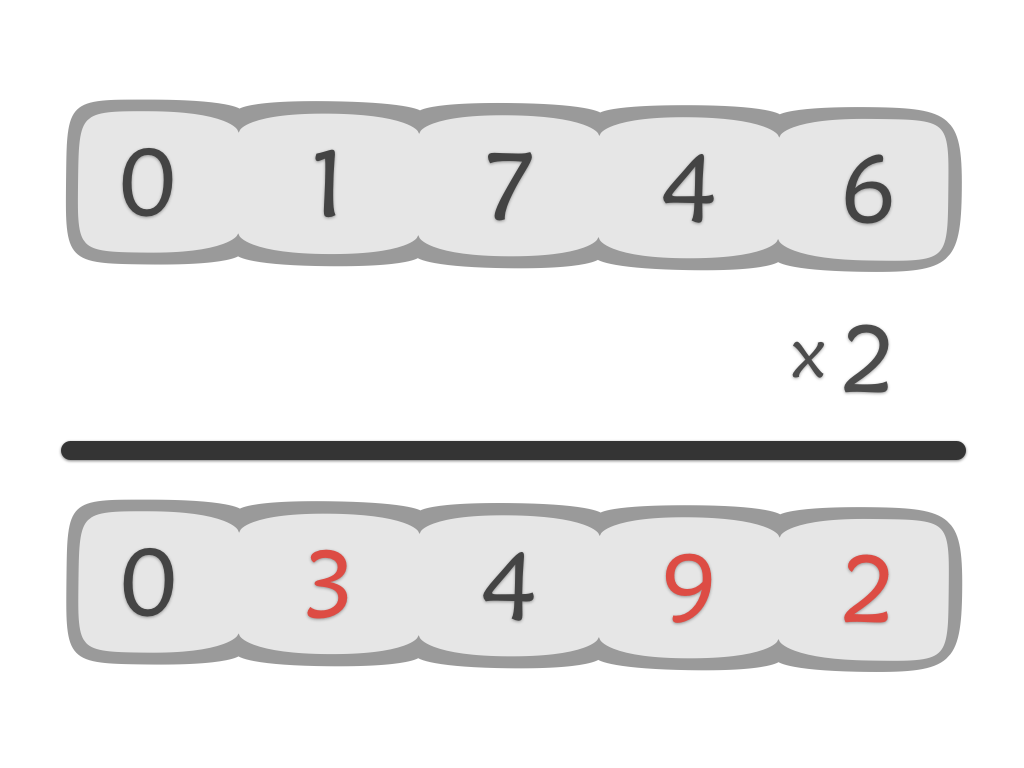
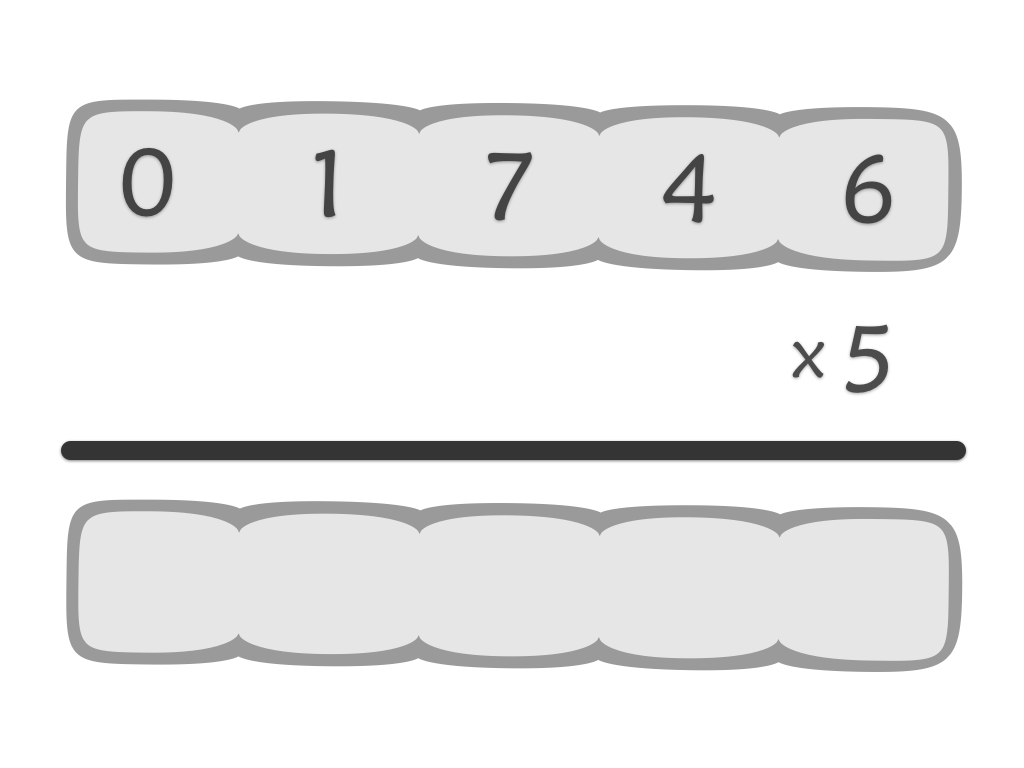
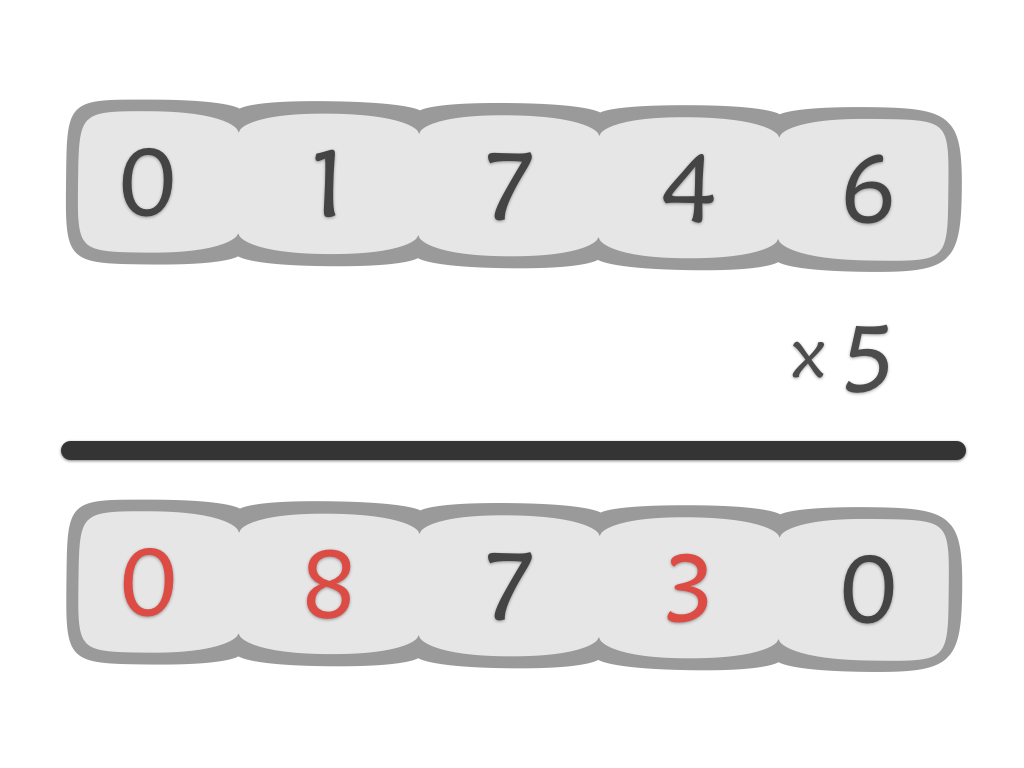
Multiplication

Escape from King Minos

The Collatz conjecture from 1937 is essential in every student’s experience of mathematics. Here we present it with a backdrop from Greek mythology.

It gives students practice in multiplying by 3 so when the bulk of your class is ready to learn 3 x 17 = 51 is the perfect time to use it.

Printable puzzle-sheets here.

Beetle Blitz

We learn best through hard fun. These games are for students who need practice with single digit multiplication. They are entirely unfair – almost always one beetle will have a winning strategy. I love to emphasize this to help remove the stigma of failure from the classroom. The beetle to beetle confrontations are entirely unfair because almost always one beetle will have a sure win. However, finding that win is hard fun.

Printable sheets here.

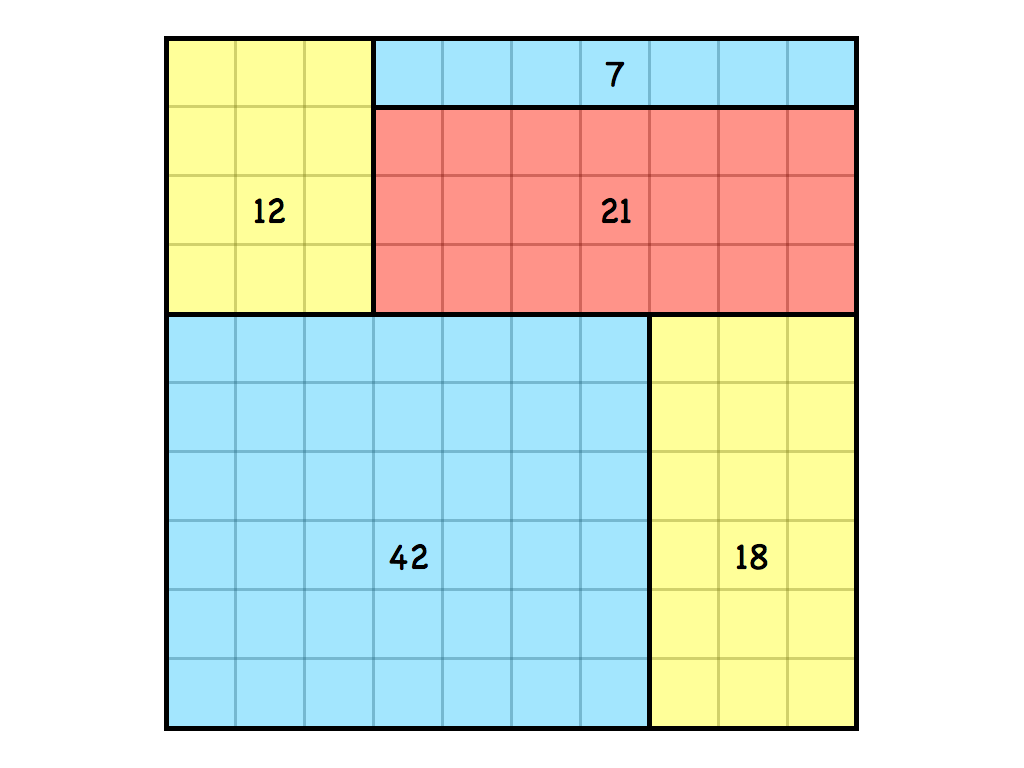
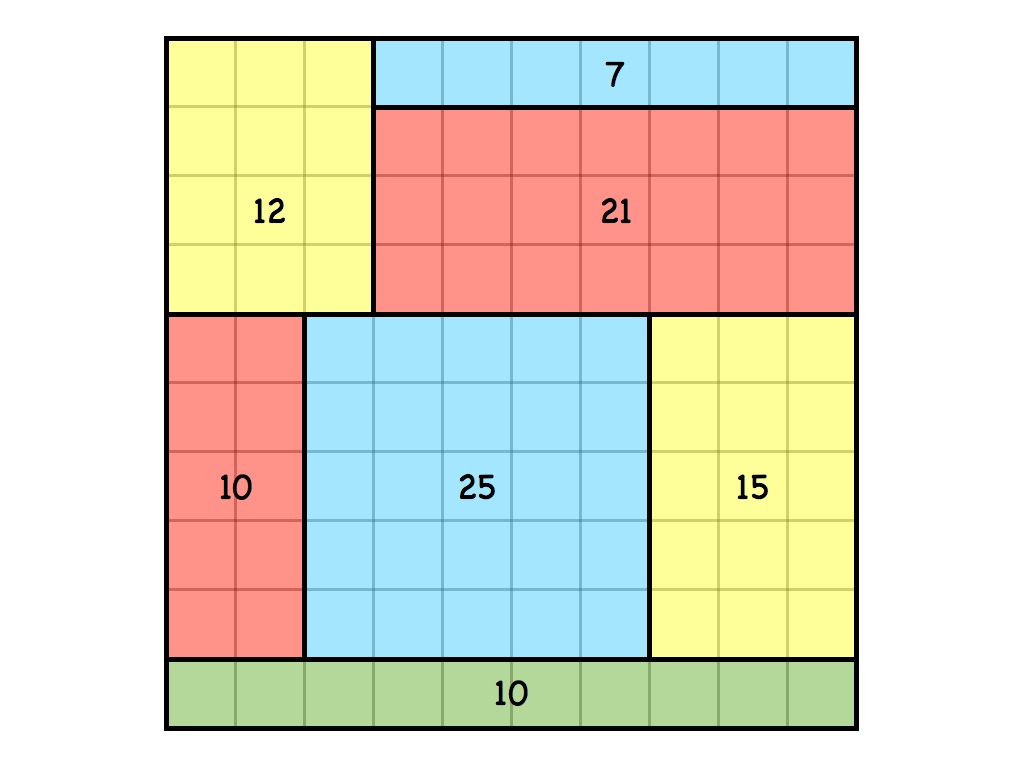
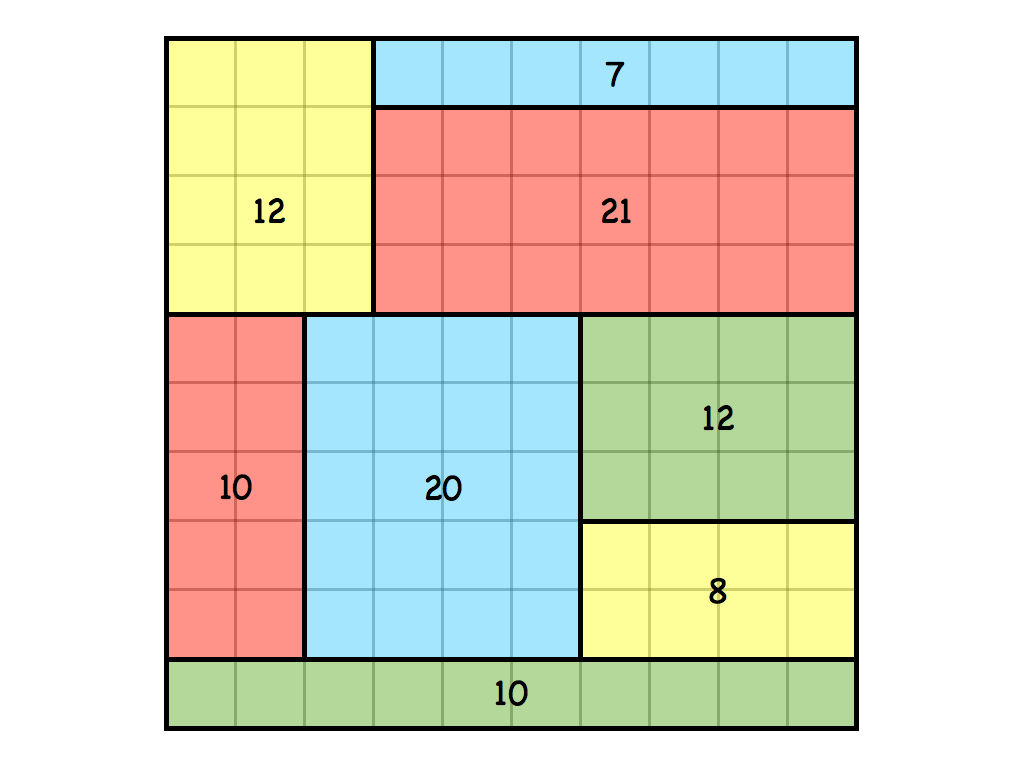
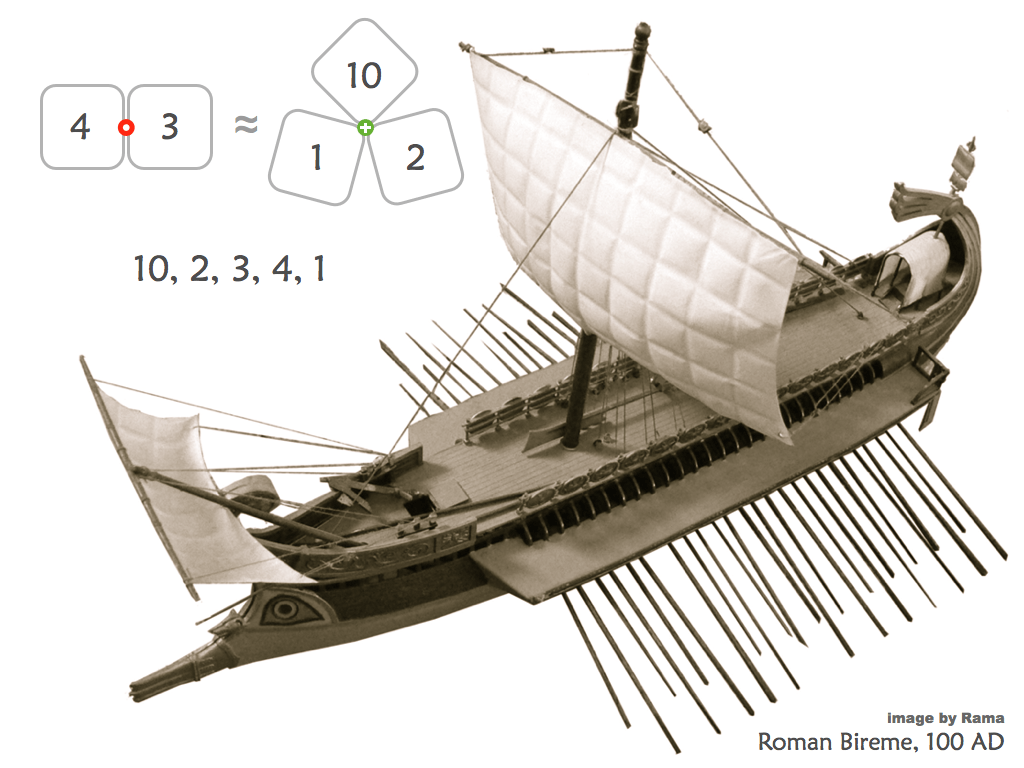
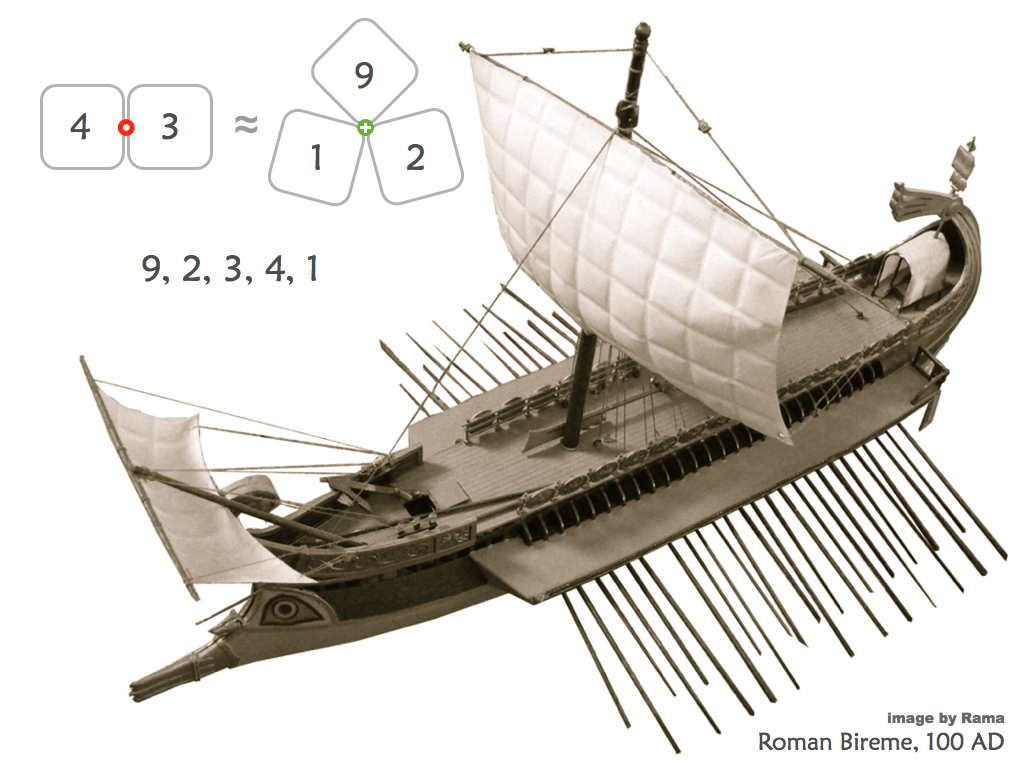
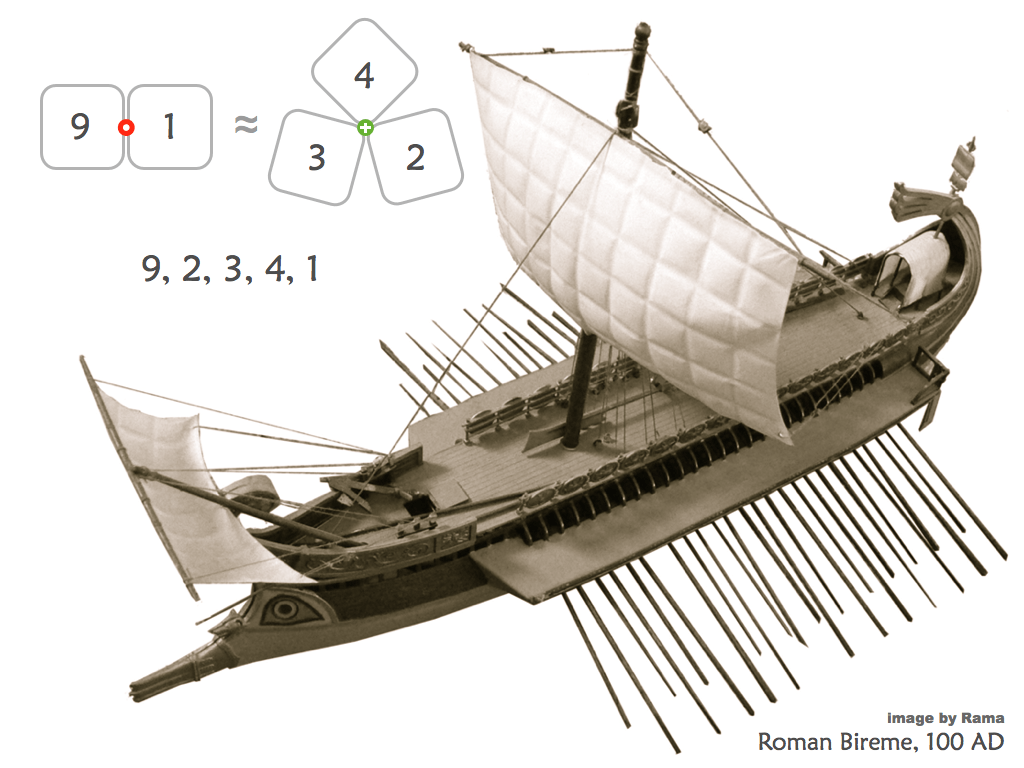
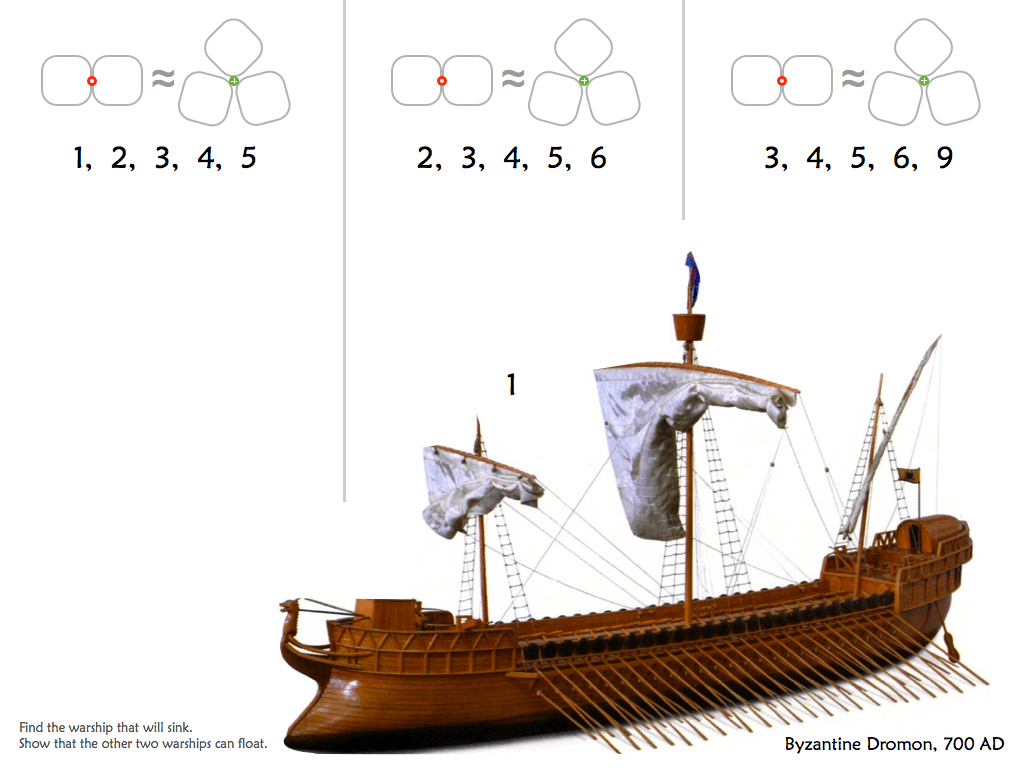
Cartouche Puzzles

These versatile puzzles are great for adults and children alike. They are based on KenKen puzzles, but are superior for the classroom because they offer engaging ways to get at age-appropriate arithmetic skills.

Printable black & white Cartouche puzzles here.

Printable colour Cartouche puzzles here.

Mondrian Art Puzzles

People who gaze upon a piece of Mondrian art should ask how he decided which colors to paint where. The disgruntled person may even ask what the piece of artwork might have looked like if Mondrian had taken the time to color it all in…

In these puzzles you’ll be Mondrian’s nasty mathematical boss. Instead of allowing Mondrian to randomly draw rectangles and colors - you lay out precise requirements...

Before we start... here is a real section of a piece of Mondrian art. You should google him to see more, because the art work that we produce is only going to be a fun imitation of the real thing.

Mondrian must cover the canvass with rectangles.

Here he has been successful, but it is not a very good solution. Why?

Mondrian's score is equal to the area of the largest rectangle minus the area of the smallest rectangle. This score must be made as small as possible. Here it is 42 - 7 = 35 which is much too large.

This is a better solution. Here Mondrian's score is 30 - 7 = 23 which is still too large, but much better than before.

This is still better a solution. Here Mondrian's score is 25 - 7 = 18.

This might look like the best solution yet, but it is not. It violates the second rule:

No two rectangles can have the same dimensions. Here we have a 3x4 and a 4x3 rectangle. That's a disaster.

PS. The 2x6 rectangle is different from the 3x4 rectangle, so those two can co-habit the same solution.

When you are introducing the Mondrian Art Puzzles, do not start with the rules. Instead start with asking one student after another to determine the dimension of one of the tiling rectangles.

This technique is true in all MathPickle puzzles. The first thing to do is focus on engagement. You do this by having students participate in a ridiculous attempt at solving a problem for which they have not even been told the rules.

The second advantage of this technique is it gives the class practice failing.

This is the first puzzle-sheet. All students should start with the 4x4. Students may not use erasers. They have three attempts to try to find the lowest possible score.

Danger: Many teachers allow fast students to streak ahead. This can be demotivating to slow, methodical thinkers. To avoid this in your classroom, allow slower students - after they complete the 4x4 - to jump up to a larger square than anyone else is working on.

The last rule is that the solutions must be colored using the fewest number of colors possible so that no two rectangles of the same color touch along an edge or vertex.

This aesthetic puzzle-within-a-puzzle increases engagement levels for those students who appreciate beauty. If any of these students wants to redo their messy sheet - give them a new sheet to let them create something of beauty.

Reward answers that are most beautiful as well as having the lowest score.

There are additional puzzle-sheets in this pdf.

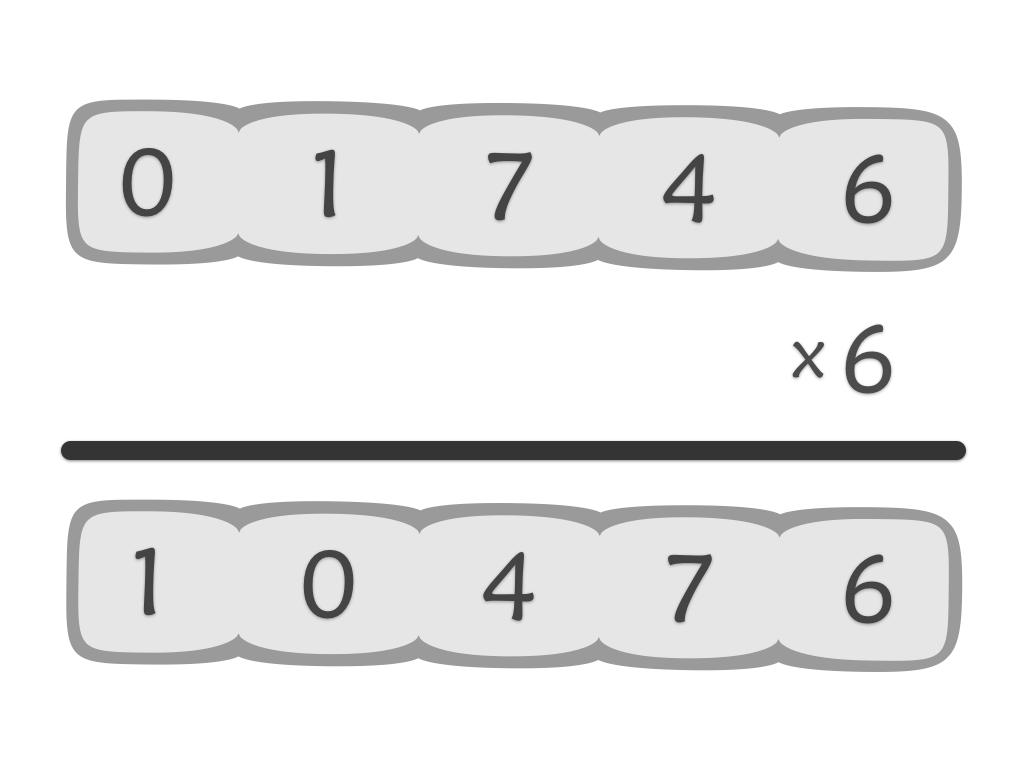
The persistence of an integer is the number of times you can perform the following before ending up at a single digit:

1) Take the digits of the integer and multiply them together to give a new integer.

2) Repeat #1 using the new integer.

Recreational mathematics is on the fringes of mathematics, but its real worth is in mathematical pedagogy. Vampire Numbers are a perfect example. They are ridiculous. Most mathematicians would not take time to look at them because they lead to little else of interest. They’re a DEAD end.

But like a lot of recreational mathematics, their true home is in the classroom where their weirdness is an asset.

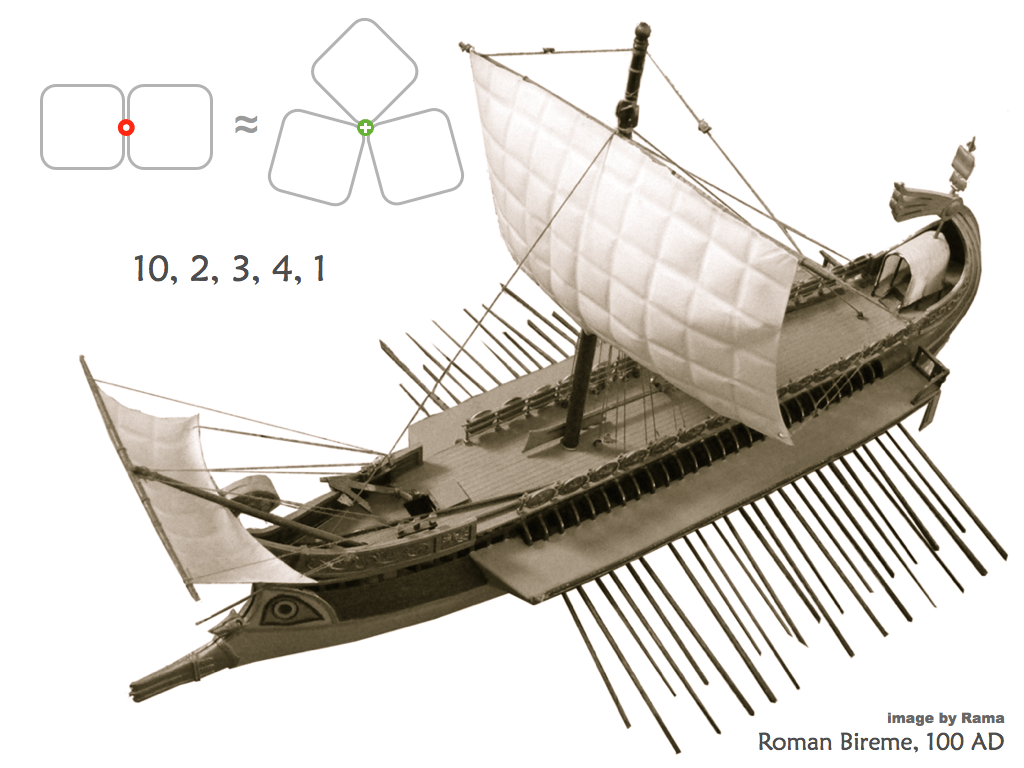
Symbiotic Sets

These are difficult puzzles – not the puzzle you want to start exploring multiplication, but there are rich ideas here that are worthy of exploration. I now call these puzzles Lichen Puzzles…

Download printable Lichen Puzzles here.

Lazy Lemur Multiplication

Let's start with an example. 01746 is good for lazy lemur multiplication because you can multiply it by a digit greater than one so that all five digits get shuffled, but remain the same.

Students are lazy lemurs. As soon as they discover that a product produces an incorrect digit, they should stop and try multiplying with a different number...

Printable puzzle-sheets here.

Does this work?

No! The result is that 01746 multiplied by two does not end up with the digits 0,1,7,4,6 shuffled. There is a 2, 3 and 9.

It is important that the students not complete the multiplication as I have done on the left. They should stop as soon as they find an incorrect digit. The reason is twofold...

1) It is fun to call the lemur's (your students) lazy. This adds to the story and to the fun.

2) By forcing students to stop (and be lazy) if they see an incorrect digit, you are creating the good habit of getting students to think as they are performing an algorithm. Too often algorithms are applied without thought.

Students do not have to be methodical, but you may choose to congratulate a student that systematically searches for the digit 2-9 to multiply 01746. Here I've decided not to be systematics. Does 5 work?

Alas - 5 does not work either.

Does 6 work?

Yes! This produces a shuffling of the digits 0,1,7,4, and 6.

I'll leave you with one other puzzle - a lot more are to be found on the puzzle-sheets that can be downloaded on the first slide.

The answer here must shuffle the digits 1,0,9,8,9 so the answer will have two nines.

Enjoy encouraging your class to be lazy!

Ballast Puzzles

The objective of this puzzle is to find those warships that will tip over because of improper ballast. Start by getting them to understand ballast... It is something heavy that you put in the bottom of a boat so it doesn't tip. I sometimes do a demo with a plastic drinking cup. How can you get it to sit up straight in the water? After they understand what it is - ask what would happen if they added too much ballast 😉 That will get everyone engaged.

Draw the five squares on the board, but explain nothing. Ask five students for numbers 1-10.

Printable puzzle-sheets here.

Numbers can be duplicated, but in this case the students chose 10, 2, 3, 4, 1. Now ask the next student which number they want to put in the leftmost square.

PS. They still know none of the rules. Rules introduced too early can bore. Much better to let students guess at what the rules might be for 30 seconds.

Five students in order of seating have put the numbers in the squares. Now you explain that the red dot is multiplication and the green plus is addition and ask them if this warship will sink or float? Is it balanced?

4 x 3 versus 10 + 1 + 2

That seems balanced you might comment. The next student is chosen to answer if he or she thinks it will sink or float. This one will sink because the right side (13) is too heavy. Disaster! Identify the students who failed with a wry grin - of course they failed - they didn't even know the rules!

Notice that you are NOT giving students the option to participate. Hands are not raised and fast students must be controlled not to blurt out the answer thereby robbing slower students of their turn in the sun.

Fast students will be frustrated, but after working with them for a week, they realize that their time will come in the second part of the class when students work alone or in pairs.

The original problem looked hopeless. Let the students discover this. It is MUCH better to start with a Disaster - it is so much more engaging. One student wanted me to replace the 10 with a 9. I did that.

Another student raised her hand. This is okay - it is an insight that she has rather than butting in on another student. She said there was another solution and she was right.

Students do not often start out comfortable enough to share and explore. This class I had been teaching for about 10 periods.

I do not congratulate the girl, rather all the focus is on what a relief it must be to the sailors. Keep the veneer of story alive!

Now it is time for the puzzle-sheets. In each one there are three warships. Two can be made to float. One will sink no matter what desperate measures you try.

So many students come into math class with some goody-goody mumbo-jumbo about everything being possible if they just try hard enough. I like to break them out of that mind-set with humour. Just like in real life - not everything is possible 😉

See my pinterest multiplication page for bad and good discoveries from the web.